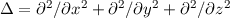 in Kugelkoordinaten, d.h. in der Darstellung (siehe Gl. (11.7))
in Kugelkoordinaten, d.h. in der Darstellung (siehe Gl. (11.7))
In Abschnitt 11.1 benützten wir den Laplace-Operator 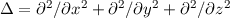 in Kugelkoordinaten, d.h. in der Darstellung (siehe Gl. (11.7))
in Kugelkoordinaten, d.h. in der Darstellung (siehe Gl. (11.7))
In diesem Abschnitt nehmen wir nun diese Umrechnung des Laplace-Operators von kartesischen zu Kugelkoordinaten vor. Dazu verwenden wir die folgenden Transformationsregeln
bzw. die Umkehrung
Wir gehen nun schrittweise vor, indem wir als erstes die erste Ableitung von
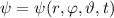 nach
nach  , dann die zweite Ableitung von
, dann die zweite Ableitung von 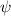 nach
nach  und
anschliessend die entsprechenden Ableitungen für
und
anschliessend die entsprechenden Ableitungen für 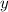 und
und  bestimmen.
bestimmen.

Mit
erhalten wir

Für die zweite Ableitung von 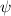 nach
nach  ergibt sich mit (F.12)
ergibt sich mit (F.12)
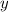
Mit
erhalten wir
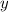
Für die zweite Ableitung von 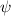 nach
nach 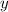 ergibt sich mit (F.18)
ergibt sich mit (F.18)

Mit
erhalten wir

Für die zweite Ableitung von 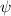 nach
nach  ergibt sich mit (F.24)
ergibt sich mit (F.24)
Der Laplace-Operator 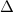 in Kugelkoordinaten entspricht nun der Summe der
Ausdrücke (F.13), (F.19) und (F.25). D.h. es gilt
in Kugelkoordinaten entspricht nun der Summe der
Ausdrücke (F.13), (F.19) und (F.25). D.h. es gilt
Um die Formelschlacht ein bisschen übersichtlicher zu gestalten, verzichten wir auf
das direkte Einsetzen und vereinfachen in der Summe (F.13) + (F.19) + (F.25) die
Ausdrücke, welche nur die zweite Ableitung nach  ,
, 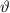 oder
oder 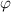 enthalten,
Ausdrücke, welche nur die erste Ableitung nach
enthalten,
Ausdrücke, welche nur die erste Ableitung nach  ,
, 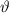 oder
oder 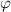 enthalten oder
Ausdrücke, welche nur eine gemischte Ableitung nach
enthalten oder
Ausdrücke, welche nur eine gemischte Ableitung nach  und
und 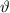 ,
,  und
und 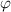 oder
oder 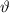 und
und 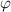 enthalten, separat:
enthalten, separat:

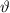
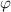

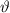
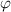
 und
und 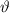
 und
und 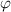
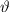 und
und 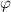
Mit den Vereinfachungen i) - ix) ergibt sich für die Summe (F.13) + (F.19)
+ (F.25), d.h. für den Laplace-Operator 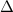 (F.26) in Kugelkoordinaten das
folgende Resultat
(F.26) in Kugelkoordinaten das
folgende Resultat
Dieser Ausdruck stimmt mit (F.1) überein, womit die Richtigkeit von (F.1) gezeigt ist.