Das Verständnis des einfachsten Atoms, d.h. des Wasserstoffatoms, ist eine der
Grundlagen zum Verständnis aller Atome. Die theoretische Behandlung des
Wasserstoffatoms ist zudem eine der schönsten Illustrationen zur Anwendung der
Quantenmechanik. Insbesondere können viele Begriffe, die dabei erarbeitet werden,
auf andere Systeme übertragen werden.
Wie wir in Kapitel 8 gesehen haben, liefert das (semiklassische) Bohrsche
Atommodell bereits eine gute Beschreibung der grundlegenden Eigenschaften des
Spektrums des Wasserstoffatoms. In diesem Modell werden die Energieniveaus durch
die Hauptquantenzahl 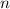 charakterisiert und die Frequenzen der Spektrallinien
sind durch die Rydberg-Formel gegeben. Das Modell stösst jedoch bei der
Beschreibung von Atomen mit mehreren Elektronen an seine Grenzen (siehe
Abschnitt 8.6). Auch die Beschreibung des Wasserstoffspektrums ist nur begrenzt
möglich, was bei einer detaillierten Betrachtung des Spektrums klar wird. Es
treten viele nach dem Bohrschen Atommodell nicht erwartete Spektrallinien
auf.
charakterisiert und die Frequenzen der Spektrallinien
sind durch die Rydberg-Formel gegeben. Das Modell stösst jedoch bei der
Beschreibung von Atomen mit mehreren Elektronen an seine Grenzen (siehe
Abschnitt 8.6). Auch die Beschreibung des Wasserstoffspektrums ist nur begrenzt
möglich, was bei einer detaillierten Betrachtung des Spektrums klar wird. Es
treten viele nach dem Bohrschen Atommodell nicht erwartete Spektrallinien
auf.
In diesem Kapitel kommen wir nun zu einer rein quantenmechanischen Behandlung
des Wasserstoffatoms ausgehend von der Schrödinger-Gleichung. Wir werden sehen,
dass im Vergleich zum Bohrschen Atommodell zusätzliche Quantenzahlen notwendig
sind, um die Energieniveaus und die Spektrallinien zu beschreiben. Wie in
Abschnitt 8.5 angedeutet, wird dabei der Bahndrehimpuls des Elektrons
eine Rolle spielen. Ebenfalls einen Einfluss auf das Spektrum wird der
Spin
des Elektrons und des Protons haben. Zusätzlich können von aussen
angelegte elektrische und magnetische Felder, sowie die sogenannten
Vakuumfluktuationen
die Energieniveaus und Spektrallinien beeinflussen.
Wir beginnen mit der Auflistung der Annahmen, die wir für unser Modell treffen
werden und dem Aufstellen der Schrödinger-Gleichung. Anschliessend folgt das Lösen
der Schrödinger-Gleichung und somit die Bestimmung der Wellenfunktionen und der
Energieniveaus des Wasserstoffatoms.
Das Wasserstoffatom besteht aus einem Kern (Proton) mit der Masse 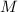 und der
Ladung
und der
Ladung 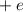 und aus einem Elektron der Masse
und aus einem Elektron der Masse 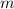 und der Ladung
und der Ladung 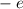 (siehe
Abb. 11.1).
(siehe
Abb. 11.1).
Für unser Modell zur Beschreibung des Wasserstoffatoms treffen wir die folgenden
Annahmen:
- Das Elektron wird als nicht-relativistisches Teilchen betrachtet.
- Der Spin des Elektrons und das damit verbundene magnetische Moment
wird vernachlässigt.
- Der Spin des Protons und das damit verbundene magnetische Moment
wird vernachlässigt.
- Vakuumfluktuationen werden nicht berücksichtigt.
- Die Wechselwirkung zwischen Elektron und Proton ist durch die
Coulomb-Wechselwirkung gegeben, d.h. die potentielle Energie entspricht dem
Coulomb-Potential
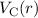 und nimmt daher die folgende Form an
und nimmt daher die folgende Form an
Es ist jedoch zu bemerken, dass dieser Ausdruck nur dann für alle Abstän-de
 gilt, wenn Kern und Elektron als Punktladungen betrachtet werden können.
Wenn aber zum Beispiel der Kern einen endlichen Radius
gilt, wenn Kern und Elektron als Punktladungen betrachtet werden können.
Wenn aber zum Beispiel der Kern einen endlichen Radius 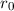 besitzt, dann ist
die
besitzt, dann ist
die 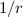 -Abhängigkeit als Näherung zu betrachten, die nur dann angewendet
werden darf, wenn die Aufenthaltswahrscheinlichkeit des Elektrons innerhalb
-Abhängigkeit als Näherung zu betrachten, die nur dann angewendet
werden darf, wenn die Aufenthaltswahrscheinlichkeit des Elektrons innerhalb
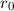 vernachlässigbar ist. Beim Wasserstoffatom ist die
vernachlässigbar ist. Beim Wasserstoffatom ist die 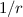 -Näherung für alle
Zustände des Elektrons gerechtfertigt.
-Näherung für alle
Zustände des Elektrons gerechtfertigt.
- Die Masse
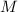 des Protons ist viel grösser als die Masse
des Protons ist viel grösser als die Masse 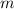 des Elektrons. Aus
diesem Grund vernachlässigen wir die Bewegung des Protons, d.h. das Proton
ist in Ruhe. Soll die Kernbewegung berücksichtigt werden, so kann analog zu
Abschnitt 8.4.2 die Elektronenmasse
des Elektrons. Aus
diesem Grund vernachlässigen wir die Bewegung des Protons, d.h. das Proton
ist in Ruhe. Soll die Kernbewegung berücksichtigt werden, so kann analog zu
Abschnitt 8.4.2 die Elektronenmasse 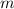 durch die reduzierte Masse
durch die reduzierte Masse
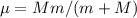 und zusätzlich die Koordinaten des Elektrons
und zusätzlich die Koordinaten des Elektrons  ,
,
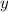 und
und  durch Relativkoordinaten
durch Relativkoordinaten 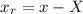 ,
, 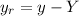 und
und
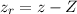 ersetzt werden. Dabei bezeichnen
ersetzt werden. Dabei bezeichnen  ,
,  und
und 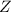 die
Koordinaten des Protons und das Atom wird im Schwerpunktssystem
betrachtet.
die
Koordinaten des Protons und das Atom wird im Schwerpunktssystem
betrachtet.
Da das Problem kugelsymmetrisch ist, führen wir Kugelkoordinaten ein (siehe
Abb. 11.1). Es gilt
Die potentielle Energie 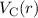 hängt nicht explizit von der Zeit ab. Daher ist die
Gesamtenergie
hängt nicht explizit von der Zeit ab. Daher ist die
Gesamtenergie 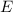 eine Konstante und es existieren stationäre Zustände der
Form
eine Konstante und es existieren stationäre Zustände der
Form
wobei 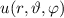 die zeitunabhängige Schrödinger-Gleichung
die zeitunabhängige Schrödinger-Gleichung
erfüllt. Der Laplace-Operator 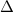 nimmt dabei in Kugelkoordinaten die folgende
Form an (siehe Anhang F)
nimmt dabei in Kugelkoordinaten die folgende
Form an (siehe Anhang F)
Einsetzen von (11.1) und (11.7) in (11.6) ergibt für die zeitunabhängige
Schröd-inger-Gleichung in Kugelkoordinaten
Bevor wir im nächsten Abschnitt die Schrödinger-Gleichung lösen, führen wir den
Bahndrehimpulsoperator 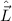 ein. Nach (9.68) lautet der Bahndrehimpulsoperator
ein. Nach (9.68) lautet der Bahndrehimpulsoperator 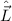 in Kugelkoordinaten
in Kugelkoordinaten
Für das Quadrat des Bahndrehimpulsoperators 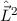 ergibt sich damit (Ausführung
der Rechnung siehe Anhang G)
ergibt sich damit (Ausführung
der Rechnung siehe Anhang G)
Damit können wir die Schrödinger-Gleichung (11.8) in der folgenden Form
schreiben
Für die Bahndrehimpulskomponenten 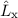 ,
, 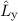 und
und 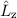 , für das Quadrat des
Bahndrehimpulsoperators
, für das Quadrat des
Bahndrehimpulsoperators 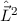 , sowie den Hamilton-Operator
, sowie den Hamilton-Operator 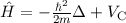 des
Wasserstoffatoms gelten dabei die folgenden Kommutatorrelationen (siehe
Abschnitt 9.3.3 und Anhang H)
des
Wasserstoffatoms gelten dabei die folgenden Kommutatorrelationen (siehe
Abschnitt 9.3.3 und Anhang H)
Das bedeutet für das Wasserstoffatom, dass Funktionen existieren, die gleichzeitig
Eigenfunktionen der Operatoren 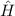 ,
, 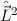 und
und 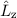 sind. D.h. die entsprechenden
Observablen
sind. D.h. die entsprechenden
Observablen 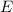 ,
, 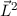 und
und 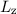 sind gleichzeitig scharf bestimmt (siehe
Abschnitt 9.5.4).
sind gleichzeitig scharf bestimmt (siehe
Abschnitt 9.5.4).
Als erstes multiplizieren wir die Schrödinger-Gleichung (11.8) mit 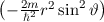 und erhalten
und erhalten
Wir wählen für die Funktion 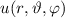 den folgenden Produktansatz
den folgenden Produktansatz
Es sei bemerkt, dass ein solcher Ansatz allgemein für alle kugelsymmetrischen
Potentiale 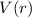 geeignet ist. Einsetzen des Ansatzes in (11.17) und Division durch
geeignet ist. Einsetzen des Ansatzes in (11.17) und Division durch
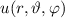 liefert
liefert
Somit hängen die einzelnen Terme der Schrödinger-Gleichung nur von einer der
Funktionen 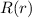 ,
, 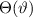 oder
oder 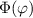 oder der Koordinate
oder der Koordinate  ab. D.h. wir konnten
durch unseren Produktansatz (11.18) die Schrödinger-Gleichung separieren. Wir
ordnen nun die Gleichung (11.19) um, so dass der Term mit
ab. D.h. wir konnten
durch unseren Produktansatz (11.18) die Schrödinger-Gleichung separieren. Wir
ordnen nun die Gleichung (11.19) um, so dass der Term mit 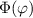 auf der rechten
Seite steht und sich alle anderen Terme auf der linken Seite befinden. Es ergibt
sich
auf der rechten
Seite steht und sich alle anderen Terme auf der linken Seite befinden. Es ergibt
sich
Diese Gleichung kann nur dann gelten, wenn die linke und rechte Seite gleichzeitig
identisch derselben Konstante sind. Wir wählen die Konstante 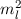 . Auf die
physikalische Bedeutung der Konstanten
. Auf die
physikalische Bedeutung der Konstanten 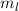 werden wir im Folgenden eingehen.
Somit lautet die Differentialgleichung zur Bestimmung von
werden wir im Folgenden eingehen.
Somit lautet die Differentialgleichung zur Bestimmung von 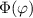
Die normierte Lösung ergibt sich zu
wobei wir den Index 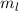 eingeführt haben. Der Vergleich mit Abschnitt 9.5.2 zeigt,
dass
eingeführt haben. Der Vergleich mit Abschnitt 9.5.2 zeigt,
dass 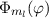 und daher auch
und daher auch 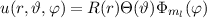 Eigenfunktionen
der z-Komponente des Bahndrehimpulsoperators
Eigenfunktionen
der z-Komponente des Bahndrehimpulsoperators 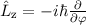 sind. Die
Eigenwertgleichung lautet
sind. Die
Eigenwertgleichung lautet
wobei aufgrund der Eindeutigkeit der Wellenfunktion 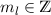 . Demzufolge
charakterisiert die Konstante
. Demzufolge
charakterisiert die Konstante 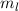 die Eigenwerte von
die Eigenwerte von 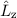 und bestimmt damit die
Werte, die der Erwartungswert der Observablen
und bestimmt damit die
Werte, die der Erwartungswert der Observablen 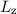 annehmen kann.
annehmen kann. 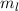 wird
magnetische Quantenzahl genannt.
wird
magnetische Quantenzahl genannt.
Als nächstes betrachten wir die linke Seite der Gleichung (11.20). Umordnen und
Division durch 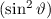 liefert
liefert
Wie zuvor kann diese Gleichung nur dann gelten, wenn die linke und rechte Seite
gleichzeitig identisch derselben Konstanten sind. Wir wählen die Konstante 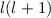 .
Auf die physikalische Bedeutung dieser neuen Konstanten
.
Auf die physikalische Bedeutung dieser neuen Konstanten 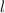 werden wir in
Abschnitt 11.2.2 eingehen. Somit ergeben sich für die Funktionen
werden wir in
Abschnitt 11.2.2 eingehen. Somit ergeben sich für die Funktionen 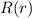 und
und 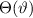 die folgenden Differentialgleichungen
die folgenden Differentialgleichungen
Aus dieser Darstellung wird insbesondere klar, dass nur die Radialkomponente 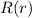 von
von 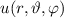 explizit vom Potential abhängt. Wir bestimmen nun die
Lösungen der Differentialgleichungen für die Funktionen
explizit vom Potential abhängt. Wir bestimmen nun die
Lösungen der Differentialgleichungen für die Funktionen 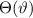 und
und 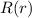 einzeln.
einzeln.
Zur Bestimmung der Lösung für die Polarkomponente 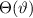 der Wellenfunktion
der Wellenfunktion
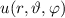 differenzieren wir die Differentialgleichung (11.27) aus und erhalten
differenzieren wir die Differentialgleichung (11.27) aus und erhalten
Wir betrachten nun  als Funktion der neuen Variablen
als Funktion der neuen Variablen 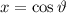 . Die
entsprechende Differentialgleichung für
. Die
entsprechende Differentialgleichung für 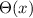 ergibt sich dann zu
ergibt sich dann zu
Lösungen dieser Differentialgleichung sind die zugeordneten Legendre-Polynome
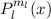 (siehe Anhang I.3)
(siehe Anhang I.3)
wobei für die Quantenzahlen 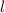 und
und 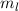 gilt
gilt
und 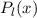 die Legendre-Polynome sind (siehe Anhang I.2), welche sich als Lösung
von (11.29) für
die Legendre-Polynome sind (siehe Anhang I.2), welche sich als Lösung
von (11.29) für 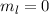 ergeben. Es gilt
ergeben. Es gilt
Die zugeordnete Legendre-Polynome 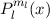 sind reell und erfüllen die folgende
Orthogonalitätsbedingung (siehe Gl. (I.33))
sind reell und erfüllen die folgende
Orthogonalitätsbedingung (siehe Gl. (I.33))
Somit lautet die normierte Lösung für die Polarkomponente 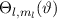 der
Wellenfunktion
der
Wellenfunktion 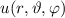 (siehe Tab. 11.1)
(siehe Tab. 11.1)
wobei wir die Indizes 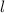 und
und 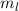 eingeführt haben und die Legendre-Polynome
eingeführt haben und die Legendre-Polynome
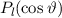 gegeben sind durch
gegeben sind durch
Mit (11.22) und (11.36) haben wir die Lösungen für 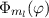 und
und 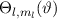 gefunden. Die Gesamtlösung des winkelabhängigen Anteils der Wellenfunktion
gefunden. Die Gesamtlösung des winkelabhängigen Anteils der Wellenfunktion
 entspricht dem Produkt dieser Funktionen. Es ergeben sich damit die
sogenannten Kugelfunktionen
entspricht dem Produkt dieser Funktionen. Es ergeben sich damit die
sogenannten Kugelfunktionen 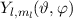 (siehe Tab. 11.2, Abb. 11.2, Abb. 11.3
und I.6)
(siehe Tab. 11.2, Abb. 11.2, Abb. 11.3
und I.6)
Tab. 11.2: Kugelfunktionen 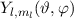 für die Quantenzahlen
für die Quantenzahlen 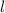 = 0, 1, 2, 3.
= 0, 1, 2, 3.
Es sei an dieser Stelle bemerkt, dass die Funktionen 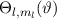 und
und 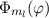 und
damit auch die Kugelfunktionen
und
damit auch die Kugelfunktionen 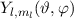 für beliebige kugelsymmetrische
Potentiale
für beliebige kugelsymmetrische
Potentiale 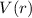 gelten, da das Potential nur explizit in der Differentialgleichung für
die Bestimmung der radialen Funktion
gelten, da das Potential nur explizit in der Differentialgleichung für
die Bestimmung der radialen Funktion 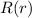 erscheint.
erscheint.
Zur Ermittlung der physikalischen Bedeutung der Quantenzahl  gehen wir zurück
zur Formulierung (11.11) der Schrödinger-Gleichung und multiplizieren sie mit
gehen wir zurück
zur Formulierung (11.11) der Schrödinger-Gleichung und multiplizieren sie mit
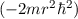
Einsetzen des Ansatzes 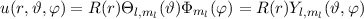 und
Division durch
und
Division durch 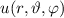 ergibt
ergibt
wobei der Vergleich mit (11.25) die linke Seite als 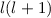 identifiziert. Damit ergibt
sich das folgende Resultat
identifiziert. Damit ergibt
sich das folgende Resultat
D.h. die Kugelfunktionen 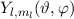 und damit die Wellenfunktionen
und damit die Wellenfunktionen 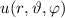 sind Eigenfunktionen des Quadrats des Bahndrehimpulsoperators
sind Eigenfunktionen des Quadrats des Bahndrehimpulsoperators 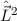 zum
Eigenwert
zum
Eigenwert 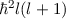 . Demzufolge charakterisiert die Quantenzahl
. Demzufolge charakterisiert die Quantenzahl 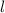 die
Eigenwerte von
die
Eigenwerte von 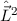 und bestimmt damit die Werte, die der Erwartungswert der
Observablen
und bestimmt damit die Werte, die der Erwartungswert der
Observablen 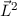 annehmen kann.
annehmen kann. 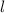 wird Bahndrehimpulsquantenzahl genannt.
Zusammenfassend können wir für den Bahndrehimpuls eines Teilchen im
kugelsymmetrischen Potential feststellen:
wird Bahndrehimpulsquantenzahl genannt.
Zusammenfassend können wir für den Bahndrehimpuls eines Teilchen im
kugelsymmetrischen Potential feststellen:
- Der Erwartungswert des Quadrats des Bahndrehimpulses
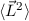 eines Teilchens,
das sich in einem kugelsymmetrischen Potential bewegt, kann nur die
diskreten Eigenwerte
eines Teilchens,
das sich in einem kugelsymmetrischen Potential bewegt, kann nur die
diskreten Eigenwerte 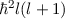 mit
mit 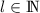 annehmen. Die entsprechende
Eigenwertgleichung lautet
annehmen. Die entsprechende
Eigenwertgleichung lautet
- Der Erwartungswert der z-Komponente des Bahndrehimpulses
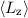 eines
Teilchens, das sich in einem kugelsymmetrischen Potential bewegt, kann nur die
diskreten Eigenwerte
eines
Teilchens, das sich in einem kugelsymmetrischen Potential bewegt, kann nur die
diskreten Eigenwerte 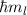 mit
mit 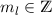 und
und 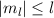 annehmen. Die
entsprechende Eigenwertgleichung lautet
annehmen. Die
entsprechende Eigenwertgleichung lautet
- Die Wellenfunktionen
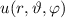 sind gleichzeitig Eigenfunktionen der drei
Operatoren
sind gleichzeitig Eigenfunktionen der drei
Operatoren 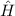 ,
, 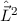 und
und 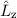 .
.
Nach den vorangegangenen Ausführungen sind durch die Bahndrehimpulsquantenzahl 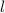 und die magnetische Quantenzahl
und die magnetische Quantenzahl 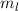 die Erwartungswerte der Observablen
die Erwartungswerte der Observablen 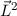 und
und 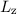 bestimmt. Befindet sich das System in einem Eigenzustand, dann
gilt
bestimmt. Befindet sich das System in einem Eigenzustand, dann
gilt
Die erste Gleichung bestimmt den Betrag des Bahndrehimpulsvektors 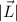 . Es
gilt
. Es
gilt
Abb. 11.4, in der die möglichen Bahndrehimpulsvektoren für die
Bahndrehimpulsquantenzahlen 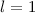 und
und 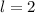 gezeichnet sind, bestätigt
die Bedingung
gezeichnet sind, bestätigt
die Bedingung 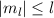 . Insbesondere kann der Vektor
. Insbesondere kann der Vektor 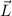 aufgrund
der Bedingungen (11.47) und (11.46) nie entlang der z-Achse zeigen.
Dies ist im Einklang damit, dass nur eine einzige Komponente, die
z-Komponente,
des Bahndrehimpulses scharf sein kann. Entlang der beiden dazu orthogonalen
Raumrichtungen, x und y, ist der Bahndrehimpuls unscharf. In anderen Worten
ausgedrückt, bedeutet das, dass wenn
aufgrund
der Bedingungen (11.47) und (11.46) nie entlang der z-Achse zeigen.
Dies ist im Einklang damit, dass nur eine einzige Komponente, die
z-Komponente,
des Bahndrehimpulses scharf sein kann. Entlang der beiden dazu orthogonalen
Raumrichtungen, x und y, ist der Bahndrehimpuls unscharf. In anderen Worten
ausgedrückt, bedeutet das, dass wenn 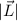 und
und 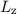 festgelegt sind, dann sind
festgelegt sind, dann sind 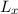 und
und 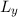 unbestimmbar.
unbestimmbar.
Wir illustrieren diesen Sachverhalt graphisch (siehe Abb. 11.5): Der Vektor 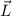 kommt
auf einer Kugel zu liegen, deren Radius durch die Bahndrehimpulsquantenzahl
kommt
auf einer Kugel zu liegen, deren Radius durch die Bahndrehimpulsquantenzahl 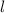 festgelegt ist (Radius =
festgelegt ist (Radius = 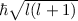 ). Die magnetische Quantenzahl
). Die magnetische Quantenzahl 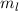 bestimmt
die z-Komponente des Bahndrehimpulses zu
bestimmt
die z-Komponente des Bahndrehimpulses zu 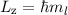 und beschränkt dadurch den
Aufenthaltsort des Vektors
und beschränkt dadurch den
Aufenthaltsort des Vektors 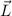 auf eine Kegelfläche innerhalb dieser Kugel. Jedoch
weiss man nicht, wo innerhalb der Kegelfläche der Vektor
auf eine Kegelfläche innerhalb dieser Kugel. Jedoch
weiss man nicht, wo innerhalb der Kegelfläche der Vektor 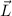 zu liegen kommt.
zu liegen kommt.
Zur Bestimmung der radialen Funktion 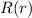 gehen wir von der
Differentialgleichung (11.26) aus, d.h. der Gleichung
gehen wir von der
Differentialgleichung (11.26) aus, d.h. der Gleichung
In dieser Gleichung tritt der Energiewert 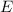 , sowie der Elektron-Kern-Abstand
, sowie der Elektron-Kern-Abstand  auf. Deshalb werden die Lösungen Auskunft über die Energie des Atoms und dessen
Grösse geben. Wir gehen dabei von gebundenen Zuständen, d.h.
auf. Deshalb werden die Lösungen Auskunft über die Energie des Atoms und dessen
Grösse geben. Wir gehen dabei von gebundenen Zuständen, d.h. 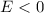 ,
aus.
,
aus.
Wir beginnen mit der Bestimmung der Funktion 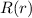 indem wir in der
Gleichung (11.48)
indem wir in der
Gleichung (11.48) 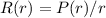 setzen. Damit ergibt sich für die Funktion
setzen. Damit ergibt sich für die Funktion 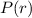 die Differentialgleichung
die Differentialgleichung
Als nächstes betrachten wir die beiden Grenzfälle  und
und 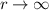 :
:
Wir setzen unsere Rechnung fort indem wir die Variable  in (11.49) durch
in (11.49) durch
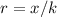 ersetzen. Gleichzeitig führen wir die Konstante
ersetzen. Gleichzeitig führen wir die Konstante 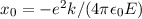 ein.
Es ergibt sich
ein.
Es ergibt sich
Wir wählen nun für 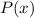 unter Berücksichtigung des Verhaltens für
unter Berücksichtigung des Verhaltens für 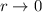 und
und
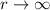 den folgenden Ansatz
den folgenden Ansatz
Einsetzen in (11.54) ergibt
Für 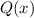 wählen wir einen Potenzreihenansatz
wählen wir einen Potenzreihenansatz
Damit erhalten wir aus (11.56)
Damit die Summe verschwindet, müssen die Koeffizienten jeder Potenz verschwinden.
Daher erhalten wir die folgende Bedingung
Damit ergibt sich zwischen den Koeffizienten die folgende Rekursionsrelation
Für hohe Potenzen, d.h. für 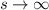 ergibt sich somit das folgende Verhalten
ergibt sich somit das folgende Verhalten
Wir vergleichen dieses Verhalten der Potenzreihe 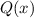 mit der Reihe
mit der Reihe
In diesem Fall ergibt sich für nachfolgende Koeffizienten das folgende Grenzverhalten
D.h. die Reihe 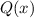 würde wie
würde wie 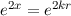 divergieren für
divergieren für 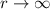 , wenn sie nicht
abbricht. Demzufolge würde
, wenn sie nicht
abbricht. Demzufolge würde 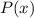 wie
wie 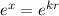 divergieren für
divergieren für 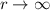 und
und 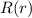 wäre nicht normierbar und daher physikalisch nicht sinnvoll. Demzufolge muss die
Reihe abbrechen. Nennen wir die höchste in der Reihe auftretende Potenz
wäre nicht normierbar und daher physikalisch nicht sinnvoll. Demzufolge muss die
Reihe abbrechen. Nennen wir die höchste in der Reihe auftretende Potenz
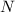 , so ergibt sich die Abbruchbedingung
, so ergibt sich die Abbruchbedingung 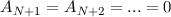 und
damit
und
damit
Die Zahl 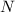 wird radiale Quantenzahl genannt. Mit
wird radiale Quantenzahl genannt. Mit 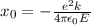 und
und
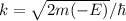 ergeben sich damit die folgenden diskreten Energiewerte
ergeben sich damit die folgenden diskreten Energiewerte
Mit der Rydberg-Energie 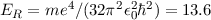 eV und der Hauptquantenzahl
eV und der Hauptquantenzahl
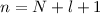 ergibt sich daraus für die Energiewerte
ergibt sich daraus für die Energiewerte 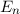 des Wasserstoffatoms
(siehe Tab. 11.3)
des Wasserstoffatoms
(siehe Tab. 11.3)
Dieses Ergebnis ist identisch zu dem des Bohrschen Atommodells. Damit hängen die
Energiewerte 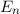 nur von der Hauptquantenzahl
nur von der Hauptquantenzahl 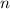 ab. Bei festem
ab. Bei festem 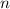 kann die
Bahndrehimpulsquantenzahl
kann die
Bahndrehimpulsquantenzahl 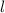 die Werte 0, 1, 2, ...,
die Werte 0, 1, 2, ..., 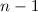 annehmen. Da zu jedem
annehmen. Da zu jedem
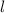 für die magnetische Quantenzahl
für die magnetische Quantenzahl 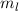
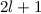 verschiedene Werte möglich
sind, ergibt sich damit der folgende Grad der Entartung des Energiewerts
verschiedene Werte möglich
sind, ergibt sich damit der folgende Grad der Entartung des Energiewerts
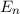
d.h. es existieren jeweils 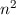 verschiedene Eigenfunktionen des Wasserstoffatoms,
charakterisiert durch die Quantenzahlen
verschiedene Eigenfunktionen des Wasserstoffatoms,
charakterisiert durch die Quantenzahlen 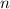 ,
, 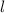 und
und 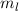 , mit derselben Energie
, mit derselben Energie 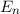 .
.
Die zu den Energiewerten 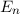 zugehörigen Funktionen
zugehörigen Funktionen 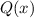 und damit die
Funktionen
und damit die
Funktionen 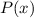 und daraus schlussendlich die radiale Funktion
und daraus schlussendlich die radiale Funktion 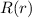 könnten mit
Hilfe der Rekursionsrelation (11.60) bestimmt werden. Wir wählen hier jedoch einen
anderen Weg: Wir schreiben die Gleichung (11.56) in eine Form, welche mit einer aus
der Mathematik bekannten Differentialgleichung übereinstimmt und übernehmen die
entsprechenden Lösungen. Die bekannte Gleichung ergibt sich aus (11.56) durch die
Substitution
könnten mit
Hilfe der Rekursionsrelation (11.60) bestimmt werden. Wir wählen hier jedoch einen
anderen Weg: Wir schreiben die Gleichung (11.56) in eine Form, welche mit einer aus
der Mathematik bekannten Differentialgleichung übereinstimmt und übernehmen die
entsprechenden Lösungen. Die bekannte Gleichung ergibt sich aus (11.56) durch die
Substitution 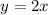 , der Definition
, der Definition 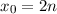 und der Multiplikation mit
und der Multiplikation mit 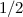 zu
zu
Diese Gleichung entspricht mit 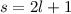 und
und 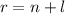 der Differentialgleichung
der zugeordneten Laguerre-Polynomen
der Differentialgleichung
der zugeordneten Laguerre-Polynomen 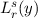 (siehe Anhang I.5)
(siehe Anhang I.5)
D.h. es gilt
wobei 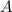 eine Normierungskonstante darstellt. Wir bestimmen nun ausgehend
von (11.70) schrittweise die normierte radiale Funktion
eine Normierungskonstante darstellt. Wir bestimmen nun ausgehend
von (11.70) schrittweise die normierte radiale Funktion 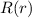 :
:
- Mit
 ergibt sich aus (11.70) für
ergibt sich aus (11.70) für 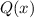
- Einsetzen in (11.55) liefert für
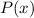
- Mit
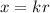 erhalten wir für
erhalten wir für 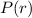 den Ausdruck
den Ausdruck
- Somit ergibt sich für die radiale Funktion
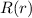
- Der letzte Schritt beinhaltet die Bestimmung der Konstanten
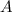 und damit die
Normierung der radialen Wellenfunktion
und damit die
Normierung der radialen Wellenfunktion 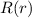 . Wir setzten dazu die
Wahrscheinlichkeit, dass das Wasserstoffatom und damit die Bahn
des Elektrons einen Radius zwischen
. Wir setzten dazu die
Wahrscheinlichkeit, dass das Wasserstoffatom und damit die Bahn
des Elektrons einen Radius zwischen 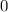 und
und 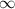 besitzt gleich
besitzt gleich 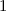
Auf diese radiale Aufenthaltswahrscheinlichkeit werden wir anschliessend bei
der Auflistung der Eigenschaften der radialen Funktionen genauer eingehen. Die
zugeordneten Laguerre-Polynome 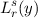 erfüllen die Normierungsbedingung
(siehe Gl. (I.60))
erfüllen die Normierungsbedingung
(siehe Gl. (I.60))
womit folgt
Daraus ergibt sich für die Konstante 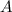
Einsetzen in (11.74) liefert für die radiale Funktion 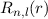
wobei wir die Quantenzahlen 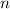 und
und 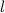 als Indizes eingeführt haben. Für
als Indizes eingeführt haben. Für 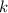 erhalten wir mit (11.66)
erhalten wir mit (11.66)
mit
dem Bohrschen Radius. Einsetzen in (11.79) liefert als Schlussresultat für die
radiale Funktion 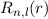 (siehe Tab. 11.4 und Abb. 11.6)
(siehe Tab. 11.4 und Abb. 11.6)
Tab. 11.4: Übersicht über die radialen Funktionen 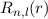 für die
Quantenzahlen
für die
Quantenzahlen 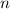 = 1, 2, 3.
= 1, 2, 3.
Die radialen Funktionen 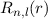 haben die folgenden Eigenschaften:
haben die folgenden Eigenschaften:
Wir gehen nun kurz auf die Eigenschaften der s-, p- und d-Funktionen ein (siehe
Tab. 11.5).
Tab. 11.5: Die Eigenfunktionen 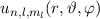 des Wasserstoffatoms für die
Hauptquantenzahlen
des Wasserstoffatoms für die
Hauptquantenzahlen 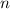 = 1, 2, 3.
= 1, 2, 3.
- Das Verständnis des Wasserstoffatoms ist eine der Grundlagen zum
Verständnis aller Atome und zudem eine der schönsten Illustrationen
der Quantenmechanik. Die rein quantenmechanische Betrachtung des
Wasserstoffatoms ausgehend von der Schrödinger-Gleichung liefert die
Antworten auf die mit dem Bohrschen-Atommodell unerklärten Aspekte.
- Das Wasserstoffatom besteht aus einem Kern (Proton) mit der Masse
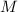 und der Ladung
und der Ladung 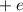 und aus einem Elektron der Masse
und aus einem Elektron der Masse 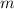 und der
Ladung
und der
Ladung 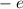 .
.
- Unserem Modell liegen im Wesentlichen folgende Annahmen zugrunde:
Das Elektron wird als nicht-relativistisches Teilchen betrachtet, der
Spin des Elektrons und des Protons und das damit verbundene
magnetische Moment wird vernachlässigt, Vakuumfluktuationen werden
nicht berücksichtigt, die Wechselwirkung zwischen Elektron und Proton
ist durch die Coulomb-Wechselwirkung gegeben und das Proton befindet
sich aufgrund der viel grösseren Masse im Vergleich zum Elektron in Ruhe.
- Unter diesen Annahmen ergeben sich für das Wasserstoffatom die
folgenden Resultate:
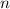 charakterisiert und die Frequenzen der Spektrallinien
sind durch die Rydberg-Formel gegeben. Das Modell stösst jedoch bei der
Beschreibung von Atomen mit mehreren Elektronen an seine Grenzen (siehe
Abschnitt 8.6). Auch die Beschreibung des Wasserstoffspektrums ist nur begrenzt
möglich, was bei einer detaillierten Betrachtung des Spektrums klar wird. Es
treten viele nach dem Bohrschen Atommodell nicht erwartete Spektrallinien
auf.
charakterisiert und die Frequenzen der Spektrallinien
sind durch die Rydberg-Formel gegeben. Das Modell stösst jedoch bei der
Beschreibung von Atomen mit mehreren Elektronen an seine Grenzen (siehe
Abschnitt 8.6). Auch die Beschreibung des Wasserstoffspektrums ist nur begrenzt
möglich, was bei einer detaillierten Betrachtung des Spektrums klar wird. Es
treten viele nach dem Bohrschen Atommodell nicht erwartete Spektrallinien
auf.
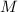 und der
Ladung
und der
Ladung 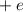 und aus einem Elektron der Masse
und aus einem Elektron der Masse 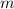 und der Ladung
und der Ladung 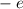 (siehe
Abb.
(siehe
Abb. 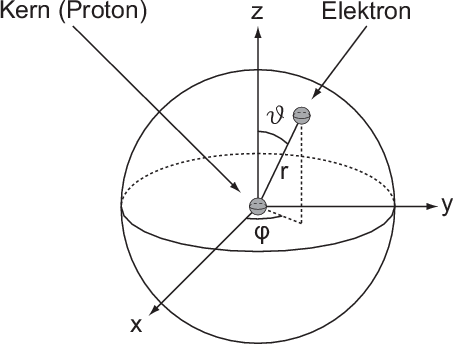
 ,
,  ,
, 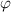 ) eingeführt.
) eingeführt.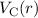 und nimmt daher die folgende Form an
und nimmt daher die folgende Form an
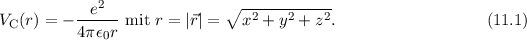
 gilt, wenn Kern und Elektron als Punktladungen betrachtet werden können.
Wenn aber zum Beispiel der Kern einen endlichen Radius
gilt, wenn Kern und Elektron als Punktladungen betrachtet werden können.
Wenn aber zum Beispiel der Kern einen endlichen Radius 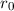 besitzt, dann ist
die
besitzt, dann ist
die 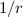 -Abhängigkeit als Näherung zu betrachten, die nur dann angewendet
werden darf, wenn die Aufenthaltswahrscheinlichkeit des Elektrons innerhalb
-Abhängigkeit als Näherung zu betrachten, die nur dann angewendet
werden darf, wenn die Aufenthaltswahrscheinlichkeit des Elektrons innerhalb
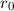 vernachlässigbar ist. Beim Wasserstoffatom ist die
vernachlässigbar ist. Beim Wasserstoffatom ist die 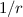 -Näherung für alle
Zustände des Elektrons gerechtfertigt.
-Näherung für alle
Zustände des Elektrons gerechtfertigt.
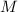 des Protons ist viel grösser als die Masse
des Protons ist viel grösser als die Masse 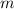 des Elektrons. Aus
diesem Grund vernachlässigen wir die Bewegung des Protons, d.h. das Proton
ist in Ruhe. Soll die Kernbewegung berücksichtigt werden, so kann analog zu
Abschnitt
des Elektrons. Aus
diesem Grund vernachlässigen wir die Bewegung des Protons, d.h. das Proton
ist in Ruhe. Soll die Kernbewegung berücksichtigt werden, so kann analog zu
Abschnitt 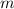 durch die reduzierte Masse
durch die reduzierte Masse
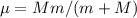 und zusätzlich die Koordinaten des Elektrons
und zusätzlich die Koordinaten des Elektrons  ,
,
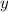 und
und  durch Relativkoordinaten
durch Relativkoordinaten 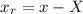 ,
, 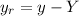 und
und
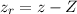 ersetzt werden. Dabei bezeichnen
ersetzt werden. Dabei bezeichnen 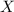 ,
, 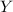 und
und 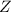 die
Koordinaten des Protons und das Atom wird im Schwerpunktssystem
betrachtet.
die
Koordinaten des Protons und das Atom wird im Schwerpunktssystem
betrachtet.
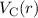 hängt nicht explizit von der Zeit ab. Daher ist die
Gesamtenergie
hängt nicht explizit von der Zeit ab. Daher ist die
Gesamtenergie 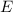 eine Konstante und es existieren stationäre Zustände der
Form
eine Konstante und es existieren stationäre Zustände der
Form

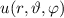 die zeitunabhängige Schrödinger-Gleichung
die zeitunabhängige Schrödinger-Gleichung
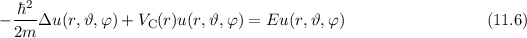
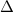 nimmt dabei in Kugelkoordinaten die folgende
Form an (siehe Anhang
nimmt dabei in Kugelkoordinaten die folgende
Form an (siehe Anhang 
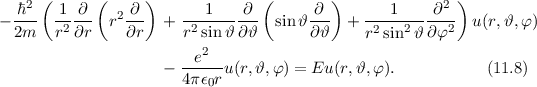
 ein. Nach (
ein. Nach (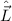 in Kugelkoordinaten
in Kugelkoordinaten
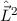 ergibt sich damit (Ausführung
der Rechnung siehe Anhang
ergibt sich damit (Ausführung
der Rechnung siehe Anhang 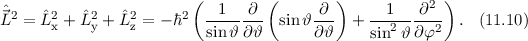
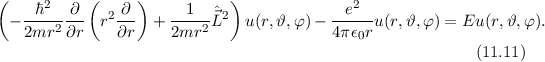
 ,
, 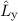 und
und 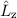 , für das Quadrat des
Bahndrehimpulsoperators
, für das Quadrat des
Bahndrehimpulsoperators 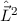 , sowie den Hamilton-Operator
, sowie den Hamilton-Operator 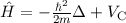 des
Wasserstoffatoms gelten dabei die folgenden Kommutatorrelationen (siehe
Abschnitt
des
Wasserstoffatoms gelten dabei die folgenden Kommutatorrelationen (siehe
Abschnitt 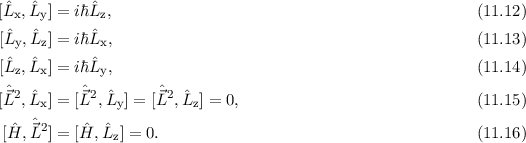
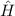 ,
, 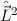 und
und 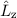 sind. D.h. die entsprechenden
Observablen
sind. D.h. die entsprechenden
Observablen 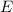 ,
, 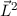 und
und 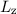 sind gleichzeitig scharf bestimmt (siehe
Abschnitt
sind gleichzeitig scharf bestimmt (siehe
Abschnitt 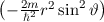 und erhalten
und erhalten
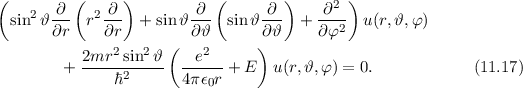
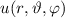 den folgenden Produktansatz
den folgenden Produktansatz

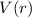 geeignet ist. Einsetzen des Ansatzes in (
geeignet ist. Einsetzen des Ansatzes in (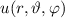 liefert
liefert
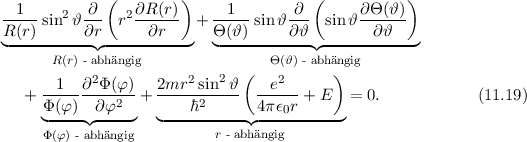
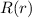 ,
, 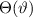 oder
oder 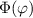 oder der Koordinate
oder der Koordinate  ab. D.h. wir konnten
durch unseren Produktansatz (
ab. D.h. wir konnten
durch unseren Produktansatz (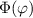 auf der rechten
Seite steht und sich alle anderen Terme auf der linken Seite befinden. Es ergibt
sich
auf der rechten
Seite steht und sich alle anderen Terme auf der linken Seite befinden. Es ergibt
sich
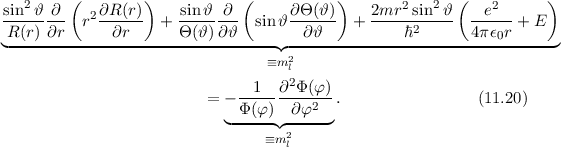
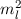 . Auf die
physikalische Bedeutung der Konstanten
. Auf die
physikalische Bedeutung der Konstanten 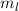 werden wir im Folgenden eingehen.
Somit lautet die Differentialgleichung zur Bestimmung von
werden wir im Folgenden eingehen.
Somit lautet die Differentialgleichung zur Bestimmung von 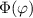


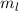 eingeführt haben. Der Vergleich mit Abschnitt
eingeführt haben. Der Vergleich mit Abschnitt 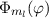 und daher auch
und daher auch 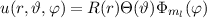 Eigenfunktionen
der z-Komponente des Bahndrehimpulsoperators
Eigenfunktionen
der z-Komponente des Bahndrehimpulsoperators 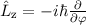 sind. Die
Eigenwertgleichung lautet
sind. Die
Eigenwertgleichung lautet

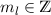 . Demzufolge
charakterisiert die Konstante
. Demzufolge
charakterisiert die Konstante 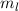 die Eigenwerte von
die Eigenwerte von 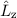 und bestimmt damit die
Werte, die der Erwartungswert der Observablen
und bestimmt damit die
Werte, die der Erwartungswert der Observablen 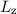 annehmen kann.
annehmen kann. 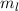 wird
wird
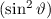 liefert
liefert
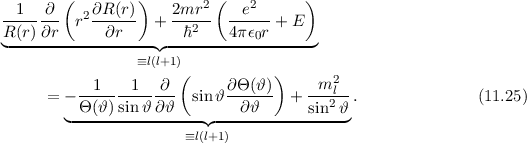
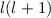 .
Auf die physikalische Bedeutung dieser neuen Konstanten
.
Auf die physikalische Bedeutung dieser neuen Konstanten 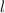 werden wir in
Abschnitt
werden wir in
Abschnitt 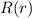 und
und 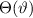 die folgenden Differentialgleichungen
die folgenden Differentialgleichungen
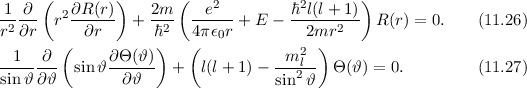
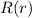 von
von 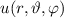 explizit vom Potential abhängt. Wir bestimmen nun die
Lösungen der Differentialgleichungen für die Funktionen
explizit vom Potential abhängt. Wir bestimmen nun die
Lösungen der Differentialgleichungen für die Funktionen 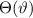 und
und 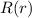 einzeln.
einzeln.
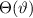 der Wellenfunktion
der Wellenfunktion
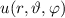 differenzieren wir die Differentialgleichung (
differenzieren wir die Differentialgleichung (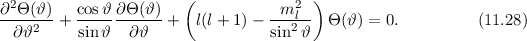
 als Funktion der neuen Variablen
als Funktion der neuen Variablen 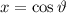 . Die
entsprechende Differentialgleichung für
. Die
entsprechende Differentialgleichung für 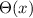 ergibt sich dann zu
ergibt sich dann zu
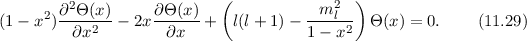
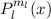 (siehe Anhang
(siehe Anhang 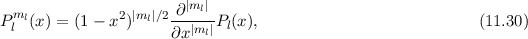
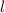 und
und 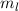 gilt
gilt
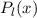 die
die 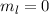 ergeben. Es gilt
ergeben. Es gilt

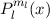 sind reell und erfüllen die folgende
Orthogonalitätsbedingung (siehe Gl. (
sind reell und erfüllen die folgende
Orthogonalitätsbedingung (siehe Gl. (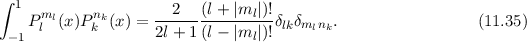
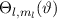 der
Wellenfunktion
der
Wellenfunktion 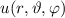 (siehe Tab.
(siehe Tab. 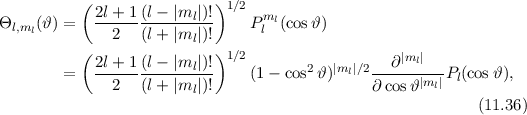
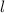 und
und 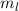 eingeführt haben und die Legendre-Polynome
eingeführt haben und die Legendre-Polynome
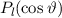 gegeben sind durch
gegeben sind durch
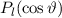
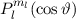
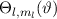
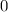
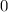
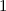
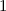
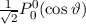
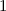
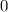
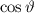
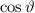
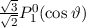
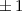
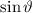
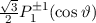
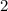
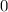
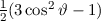
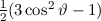
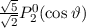
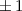
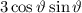
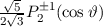
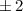
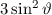
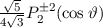
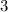
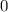
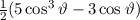
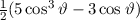
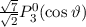
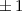
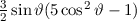
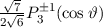
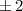
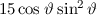
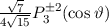
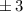
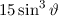
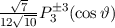
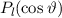 , zugeordnete Legendre-Polynome
, zugeordnete Legendre-Polynome
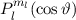 und Lösungen für die Polarkomponente
und Lösungen für die Polarkomponente 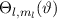 für die
Quantenzahlen
für die
Quantenzahlen 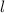 = 0, 1, 2, 3.
= 0, 1, 2, 3.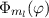 und
und 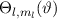 gefunden. Die Gesamtlösung des winkelabhängigen Anteils der Wellenfunktion
gefunden. Die Gesamtlösung des winkelabhängigen Anteils der Wellenfunktion
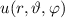 entspricht dem Produkt dieser Funktionen. Es ergeben sich damit die
sogenannten
entspricht dem Produkt dieser Funktionen. Es ergeben sich damit die
sogenannten 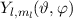 (siehe Tab.
(siehe Tab. 
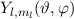
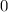
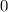
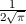
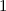
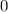
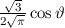
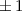
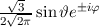
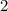
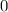
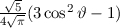
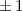
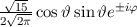
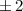
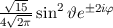
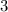
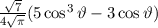
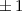
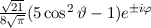
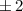
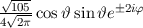
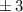
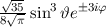
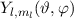 für die Quantenzahlen
für die Quantenzahlen  = 0, 1, 2, 3.
= 0, 1, 2, 3.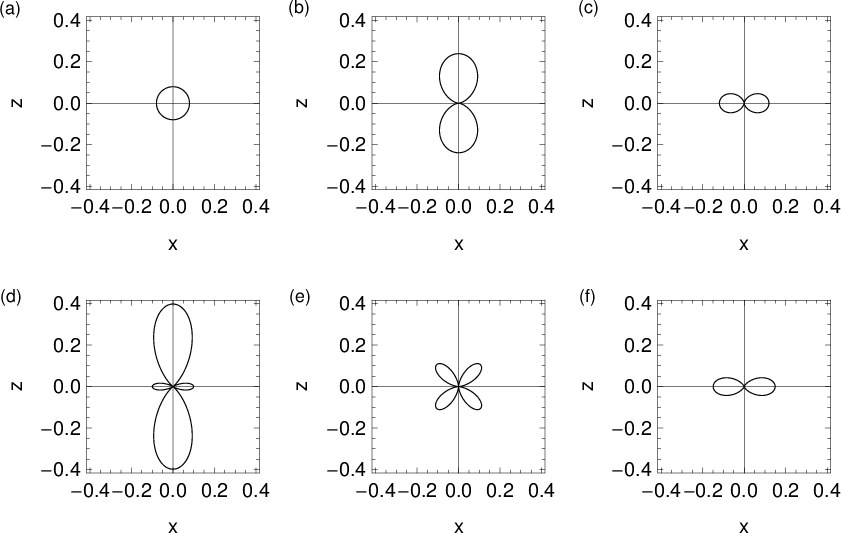
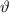 (
(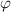 wird
0 gesetzt) wird das entsprechende Betragsquadrat der Kugelfunktionen
wird
0 gesetzt) wird das entsprechende Betragsquadrat der Kugelfunktionen
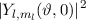 für die Quantenzahlen (a)
für die Quantenzahlen (a) 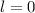 ,
, 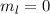 , (b)
, (b) 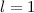 ,
, 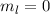 ,
(c)
,
(c) 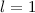 ,
, 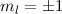 , (d)
, (d) 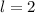 ,
, 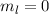 , (e)
, (e) 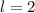 ,
, 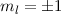 und (f)
und (f)
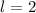 ,
, 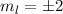 aufgetragen.
aufgetragen. 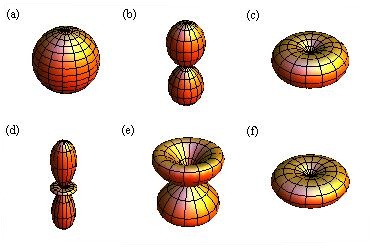
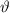 und
und 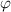 wird das
entsprechende Betragsquadrat der Kugelfunktionen
wird das
entsprechende Betragsquadrat der Kugelfunktionen 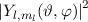 für die
Quantenzahlen (a)
für die
Quantenzahlen (a) 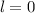 ,
, 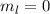 , (b)
, (b) 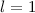 ,
, 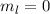 , (c)
, (c) 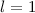 ,
, 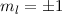 ,
(d)
,
(d) 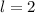 ,
, 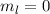 , (e)
, (e) 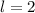 ,
, 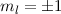 und (f)
und (f)  ,
,  aufgetragen.
aufgetragen.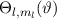 und
und 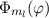 und
damit auch die Kugelfunktionen
und
damit auch die Kugelfunktionen 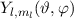 für beliebige kugelsymmetrische
Potentiale
für beliebige kugelsymmetrische
Potentiale 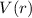 gelten, da das Potential nur explizit in der Differentialgleichung für
die Bestimmung der radialen Funktion
gelten, da das Potential nur explizit in der Differentialgleichung für
die Bestimmung der radialen Funktion 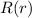 erscheint.
erscheint.
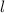 gehen wir zurück
zur Formulierung (
gehen wir zurück
zur Formulierung (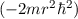
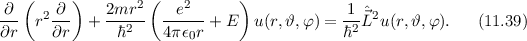
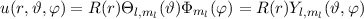 und
Division durch
und
Division durch 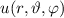 ergibt
ergibt
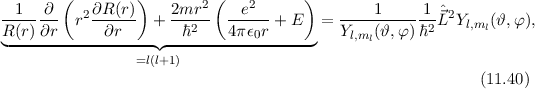
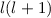 identifiziert. Damit ergibt
sich das folgende Resultat
identifiziert. Damit ergibt
sich das folgende Resultat
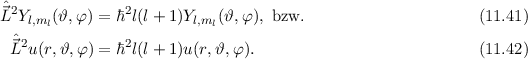
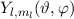 und damit die Wellenfunktionen
und damit die Wellenfunktionen 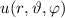 sind Eigenfunktionen des Quadrats des Bahndrehimpulsoperators
sind Eigenfunktionen des Quadrats des Bahndrehimpulsoperators 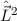 zum
Eigenwert
zum
Eigenwert 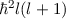 . Demzufolge charakterisiert die Quantenzahl
. Demzufolge charakterisiert die Quantenzahl 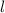 die
Eigenwerte von
die
Eigenwerte von 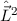 und bestimmt damit die Werte, die der Erwartungswert der
Observablen
und bestimmt damit die Werte, die der Erwartungswert der
Observablen 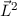 annehmen kann.
annehmen kann. 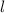 wird
wird 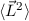 eines Teilchens,
das sich in einem kugelsymmetrischen Potential bewegt, kann nur die
diskreten Eigenwerte
eines Teilchens,
das sich in einem kugelsymmetrischen Potential bewegt, kann nur die
diskreten Eigenwerte 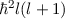 mit
mit 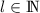 annehmen. Die entsprechende
Eigenwertgleichung lautet
annehmen. Die entsprechende
Eigenwertgleichung lautet 
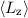 eines
Teilchens, das sich in einem kugelsymmetrischen Potential bewegt, kann nur die
diskreten Eigenwerte
eines
Teilchens, das sich in einem kugelsymmetrischen Potential bewegt, kann nur die
diskreten Eigenwerte 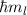 mit
mit 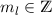 und
und 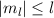 annehmen. Die
entsprechende Eigenwertgleichung lautet
annehmen. Die
entsprechende Eigenwertgleichung lautet 
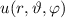 sind gleichzeitig Eigenfunktionen der drei
Operatoren
sind gleichzeitig Eigenfunktionen der drei
Operatoren 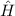 ,
, 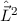 und
und 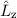 .
.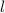 und die magnetische Quantenzahl
und die magnetische Quantenzahl 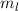 die Erwartungswerte der Observablen
die Erwartungswerte der Observablen 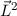 und
und 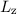 bestimmt. Befindet sich das System in einem Eigenzustand, dann
gilt
bestimmt. Befindet sich das System in einem Eigenzustand, dann
gilt

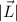 . Es
gilt
. Es
gilt

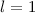 und
und 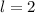 gezeichnet sind, bestätigt
die Bedingung
gezeichnet sind, bestätigt
die Bedingung 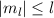 . Insbesondere kann der Vektor
. Insbesondere kann der Vektor 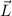 aufgrund
der Bedingungen (
aufgrund
der Bedingungen (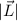 und
und 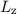 festgelegt sind, dann sind
festgelegt sind, dann sind 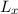 und
und 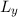 unbestimmbar.
unbestimmbar. 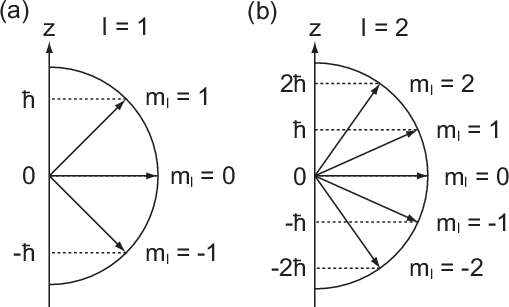
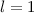 und (b)
und (b)  sind jeweils
die möglichen Bahndrehimpulsvektoren im Bezug zur z-Achse eingezeichnet.
sind jeweils
die möglichen Bahndrehimpulsvektoren im Bezug zur z-Achse eingezeichnet. kommt
auf einer Kugel zu liegen, deren Radius durch die Bahndrehimpulsquantenzahl
kommt
auf einer Kugel zu liegen, deren Radius durch die Bahndrehimpulsquantenzahl 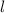 festgelegt ist (Radius =
festgelegt ist (Radius = 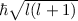 ). Die magnetische Quantenzahl
). Die magnetische Quantenzahl 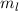 bestimmt
die z-Komponente des Bahndrehimpulses zu
bestimmt
die z-Komponente des Bahndrehimpulses zu 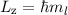 und beschränkt dadurch den
Aufenthaltsort des Vektors
und beschränkt dadurch den
Aufenthaltsort des Vektors  auf eine Kegelfläche innerhalb dieser Kugel. Jedoch
weiss man nicht, wo innerhalb der Kegelfläche der Vektor
auf eine Kegelfläche innerhalb dieser Kugel. Jedoch
weiss man nicht, wo innerhalb der Kegelfläche der Vektor  zu liegen kommt.
zu liegen kommt.
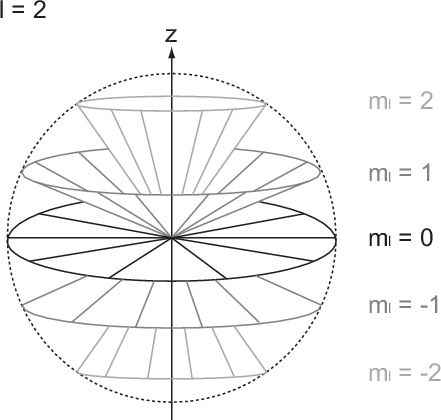
 . Durch die magnetische Quantenzahl
. Durch die magnetische Quantenzahl 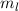 wird eine der 5 möglichen Kegelflächen (
wird eine der 5 möglichen Kegelflächen (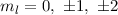 ) festgelegt, in der
der Bahndrehimpulsvektor
) festgelegt, in der
der Bahndrehimpulsvektor 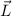 zu liegen kommt.
zu liegen kommt.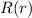 gehen wir von der
Differentialgleichung (
gehen wir von der
Differentialgleichung (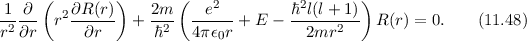
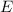 , sowie der Elektron-Kern-Abstand
, sowie der Elektron-Kern-Abstand  auf. Deshalb werden die Lösungen Auskunft über die Energie des Atoms und dessen
Grösse geben. Wir gehen dabei von gebundenen Zuständen, d.h.
auf. Deshalb werden die Lösungen Auskunft über die Energie des Atoms und dessen
Grösse geben. Wir gehen dabei von gebundenen Zuständen, d.h. 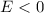 ,
aus.
,
aus.
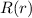 indem wir in der
Gleichung (
indem wir in der
Gleichung (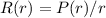 setzen. Damit ergibt sich für die Funktion
setzen. Damit ergibt sich für die Funktion 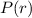 die Differentialgleichung
die Differentialgleichung
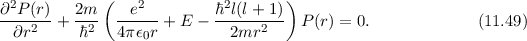
 und
und 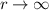 :
:
 reduziert sich die Differentialgleichung (
reduziert sich die Differentialgleichung (

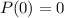 folgt
folgt 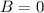 und damit
und damit 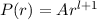 für
für
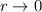 .
.
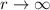 reduziert sich die Differentialgleichung (
reduziert sich die Differentialgleichung (
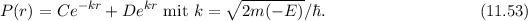
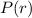 normierbar sein muss, ist
normierbar sein muss, ist 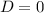 und folglich
und folglich
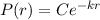 für
für 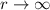 .
. in (
in (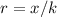 ersetzen. Gleichzeitig führen wir die Konstante
ersetzen. Gleichzeitig führen wir die Konstante 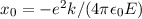 ein.
Es ergibt sich
ein.
Es ergibt sich
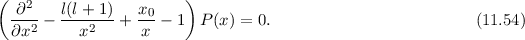
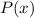 unter Berücksichtigung des Verhaltens für
unter Berücksichtigung des Verhaltens für 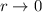 und
und
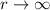 den folgenden Ansatz
den folgenden Ansatz

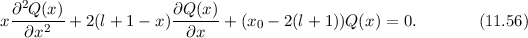
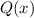 wählen wir einen Potenzreihenansatz
wählen wir einen Potenzreihenansatz

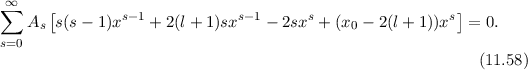
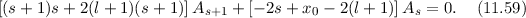

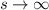 ergibt sich somit das folgende Verhalten
ergibt sich somit das folgende Verhalten

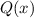 mit der Reihe
mit der Reihe

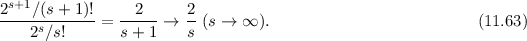
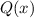 würde wie
würde wie 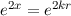 divergieren für
divergieren für 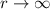 , wenn sie nicht
abbricht. Demzufolge würde
, wenn sie nicht
abbricht. Demzufolge würde 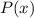 wie
wie 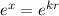 divergieren für
divergieren für 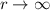 und
und 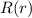 wäre nicht normierbar und daher physikalisch nicht sinnvoll. Demzufolge muss die
Reihe abbrechen. Nennen wir die höchste in der Reihe auftretende Potenz
wäre nicht normierbar und daher physikalisch nicht sinnvoll. Demzufolge muss die
Reihe abbrechen. Nennen wir die höchste in der Reihe auftretende Potenz
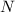 , so ergibt sich die Abbruchbedingung
, so ergibt sich die Abbruchbedingung 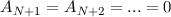 und
damit
und
damit

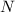 wird
wird 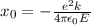 und
und
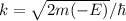 ergeben sich damit die folgenden diskreten Energiewerte
ergeben sich damit die folgenden diskreten Energiewerte

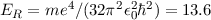 eV und der
eV und der 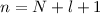 ergibt sich daraus für die Energiewerte
ergibt sich daraus für die Energiewerte 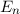 des Wasserstoffatoms
(siehe Tab.
des Wasserstoffatoms
(siehe Tab. 
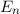 nur von der Hauptquantenzahl
nur von der Hauptquantenzahl 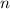 ab. Bei festem
ab. Bei festem 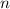 kann die
Bahndrehimpulsquantenzahl
kann die
Bahndrehimpulsquantenzahl 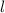 die Werte 0, 1, 2, ...,
die Werte 0, 1, 2, ..., 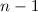 annehmen. Da zu jedem
annehmen. Da zu jedem
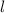 für die magnetische Quantenzahl
für die magnetische Quantenzahl 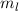
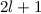 verschiedene Werte möglich
sind, ergibt sich damit der folgende Grad der Entartung des Energiewerts
verschiedene Werte möglich
sind, ergibt sich damit der folgende Grad der Entartung des Energiewerts
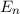
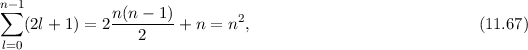
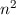 verschiedene Eigenfunktionen des Wasserstoffatoms,
charakterisiert durch die Quantenzahlen
verschiedene Eigenfunktionen des Wasserstoffatoms,
charakterisiert durch die Quantenzahlen 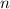 ,
, 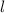 und
und 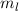 , mit derselben Energie
, mit derselben Energie 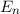 .
.
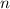
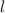
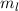
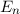
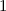
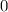
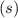
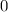
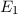
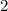
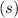
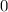
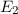
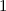
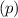
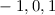
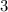
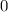
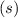
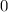
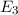
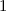
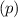
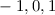
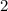
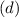
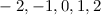
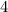
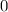
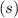
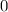
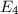
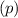
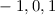
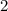
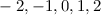
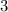
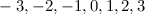
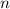

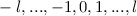
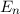
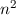 -fach
-fach 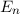 und den entsprechenden
Quantenzahlen
und den entsprechenden
Quantenzahlen 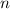 ,
, 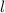 und
und 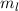 des Wasserstoffatoms. Dabei haben wir die
Werte, die die Bahndrehimpulsquantenzahl
des Wasserstoffatoms. Dabei haben wir die
Werte, die die Bahndrehimpulsquantenzahl 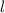 annehmen kann, wie in der
Literatur üblich, mit Buchstaben bezeichnet. Die Herkunft dieser Bezeichnungen
ist historisch bedingt. Sie ergaben sich aus der Spektroskopie:
annehmen kann, wie in der
Literatur üblich, mit Buchstaben bezeichnet. Die Herkunft dieser Bezeichnungen
ist historisch bedingt. Sie ergaben sich aus der Spektroskopie:  (
(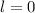 ) steht
für
) steht
für 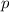 (
(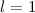 ) für
) für 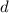 (
(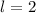 ) für
) für 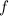 (
(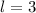 ) für
) für
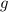 für
für 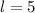 ,
, 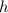 für
für 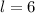 , usw..
, usw..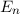 zugehörigen Funktionen
zugehörigen Funktionen 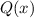 und damit die
Funktionen
und damit die
Funktionen 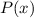 und daraus schlussendlich die radiale Funktion
und daraus schlussendlich die radiale Funktion 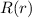 könnten mit
Hilfe der Rekursionsrelation (
könnten mit
Hilfe der Rekursionsrelation ( , der Definition
, der Definition 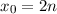 und der Multiplikation mit
und der Multiplikation mit 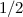 zu
zu
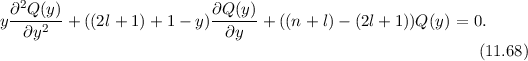
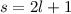 und
und 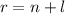 der Differentialgleichung
der
der Differentialgleichung
der 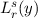 (siehe Anhang
(siehe Anhang 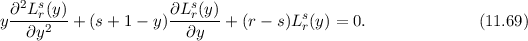

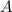 eine Normierungskonstante darstellt. Wir bestimmen nun ausgehend
von (
eine Normierungskonstante darstellt. Wir bestimmen nun ausgehend
von (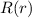 :
:
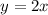 ergibt sich aus (
ergibt sich aus (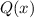

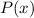
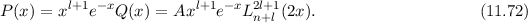
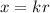 erhalten wir für
erhalten wir für 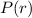 den Ausdruck
den Ausdruck 
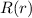
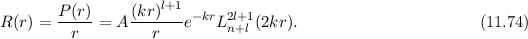
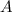 und damit die
Normierung der radialen Wellenfunktion
und damit die
Normierung der radialen Wellenfunktion 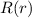 . Wir setzten dazu die
Wahrscheinlichkeit, dass das Wasserstoffatom und damit die Bahn
des Elektrons einen Radius zwischen
. Wir setzten dazu die
Wahrscheinlichkeit, dass das Wasserstoffatom und damit die Bahn
des Elektrons einen Radius zwischen 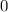 und
und  besitzt gleich
besitzt gleich 
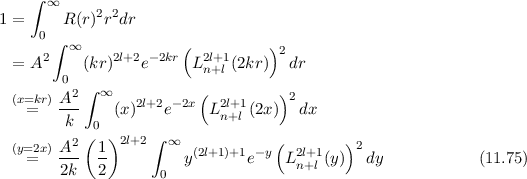
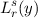 erfüllen die Normierungsbedingung
(siehe Gl. (
erfüllen die Normierungsbedingung
(siehe Gl. (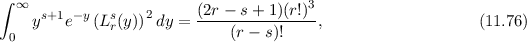

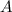
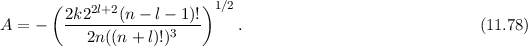
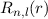
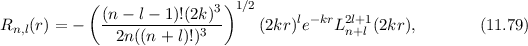
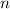 und
und 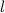 als Indizes eingeführt haben. Für
als Indizes eingeführt haben. Für 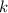 erhalten wir mit (
erhalten wir mit (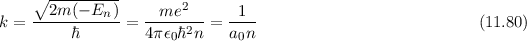

 (siehe Tab.
(siehe Tab. 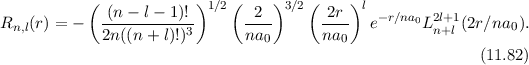
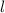
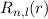
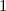
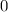
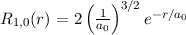
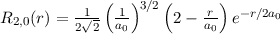
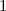
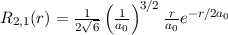
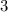
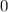
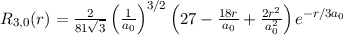
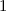
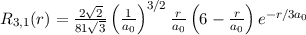
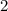
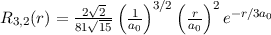
 für die
Quantenzahlen
für die
Quantenzahlen  = 1, 2, 3.
= 1, 2, 3.
 für die Quantenzahlen (a)
für die Quantenzahlen (a) 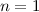 ,
,
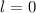 , (b)
, (b) 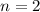 ,
, 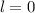 (schwarz) und
(schwarz) und 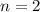 ,
, 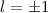 (grau), (c)
(grau), (c) 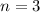 ,
,
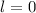 (schwarz) und
(schwarz) und 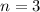 ,
, 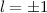 (grau) und
(grau) und 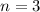 ,
, 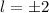 (schwarz
gestrichelt), sowie die entsprechenden radialen Aufenthaltswahrscheinlichkeiten
(schwarz
gestrichelt), sowie die entsprechenden radialen Aufenthaltswahrscheinlichkeiten
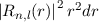 für die Quantenzahlen (d)
für die Quantenzahlen (d) 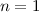 ,
, 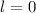 , (e)
, (e) 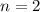 ,
, 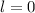 (schwarz) und
(schwarz) und 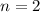 ,
, 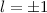 (grau), (f)
(grau), (f) 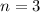 ,
, 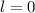 (schwarz) und
(schwarz) und
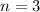 ,
, 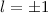 (grau) und
(grau) und 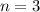 ,
, 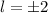 (schwarz gestrichelt).
(schwarz gestrichelt).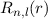 haben die folgenden Eigenschaften:
haben die folgenden Eigenschaften:
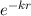 bewirkt, dass die Funktionen
bewirkt, dass die Funktionen 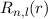 bei
bei 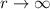 verschwinden.
verschwinden.
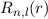 für
für 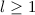 besitzen am Ursprung (
besitzen am Ursprung (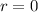 ) eine
Nullstelle.
) eine
Nullstelle.
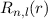 besitzen
besitzen 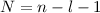 Nullstellen, die
Knotenpunkten in der Aufenthaltswahrscheinlichkeit entsprechen.
Nullstellen, die
Knotenpunkten in der Aufenthaltswahrscheinlichkeit entsprechen.
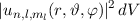 das Elektron im
Volumenelement
das Elektron im
Volumenelement 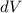 am Ort
am Ort 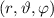 anzutreffen ist gegeben durch
anzutreffen ist gegeben durch
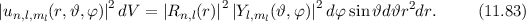
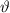 und
und 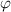 . Sie ist die Wahrscheinlichkeit, das Elektron im Intervall
. Sie ist die Wahrscheinlichkeit, das Elektron im Intervall 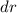 in einem
Abstand
in einem
Abstand  vom Ursprung (Kern) zu finden. Da die Funktionen
vom Ursprung (Kern) zu finden. Da die Funktionen 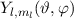 normiert sind, ist sie gegeben durch
normiert sind, ist sie gegeben durch 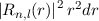 .
.
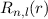 gelten nur für Potentiale
gelten nur für Potentiale 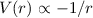 . Die
Funktionen
. Die
Funktionen 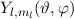 gelten hingegen für beliebige kugelsymmetrische
Potentiale
gelten hingegen für beliebige kugelsymmetrische
Potentiale 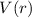 .
.
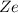 ergeben sich die Energiewerte
ergeben sich die Energiewerte
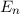 zu
zu 
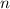
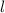
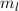
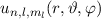
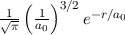
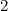
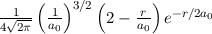
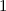
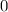
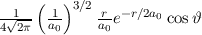

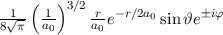
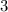
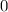
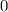
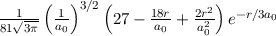
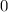
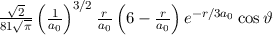

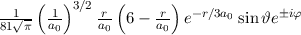
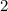
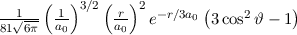

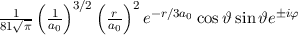
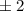
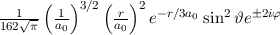
 des Wasserstoffatoms für die
Hauptquantenzahlen
des Wasserstoffatoms für die
Hauptquantenzahlen 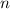 = 1, 2, 3.
= 1, 2, 3. und damit
auch
und damit
auch  . Die entsprechende Kugelfunktion
. Die entsprechende Kugelfunktion 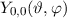 ist konstant
und dementsprechend sind die s-Funktionen kugelsymmetrisch. Weitere
Eigenschaften der s-Funktionen sind zudem, dass der Betrag des
Bahndrehimpulses verschwindet, sie als einzige am Ort des Kerns nicht
verschwinden und dass zu jedem Wert von
ist konstant
und dementsprechend sind die s-Funktionen kugelsymmetrisch. Weitere
Eigenschaften der s-Funktionen sind zudem, dass der Betrag des
Bahndrehimpulses verschwindet, sie als einzige am Ort des Kerns nicht
verschwinden und dass zu jedem Wert von 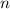 nur eine einzige s-Funktion
gehört.
nur eine einzige s-Funktion
gehört.
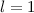 . Dann muss
. Dann muss
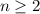 sein oder in anderen Worten, es existieren keine 1p-Funktionen
(Eigenfunktionen mit
sein oder in anderen Worten, es existieren keine 1p-Funktionen
(Eigenfunktionen mit 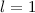 für
für 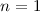 ). Die magnetische Quantenzahl
kann entsprechend die drei Werte
). Die magnetische Quantenzahl
kann entsprechend die drei Werte 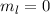 ,
,  annehmen, d.h. zu
jedem Wert von
annehmen, d.h. zu
jedem Wert von 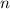 gehören drei p-Funktionen.
gehören drei p-Funktionen.
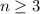 sein oder in anderen Worten, es existieren keine 1d und
2d-Funktionen (Eigenfunktionen mit
sein oder in anderen Worten, es existieren keine 1d und
2d-Funktionen (Eigenfunktionen mit 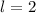 für
für 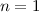 und
und 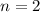 ). Die
magnetische Quantenzahl kann entsprechend die fünf Werte
). Die
magnetische Quantenzahl kann entsprechend die fünf Werte 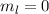 ,
,
 ,
, 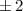 annehmen, d.h. zu jedem Wert von
annehmen, d.h. zu jedem Wert von 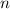 gehören fünf
d-Funktionen.
gehören fünf
d-Funktionen.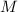 und der Ladung
und der Ladung 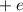 und aus einem Elektron der Masse
und aus einem Elektron der Masse 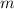 und der
Ladung
und der
Ladung 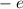 .
.
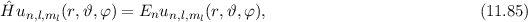
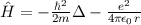 .
.
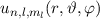 des Hamilton-Operators
des Hamilton-Operators 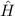 lauten
mit (
lauten
mit (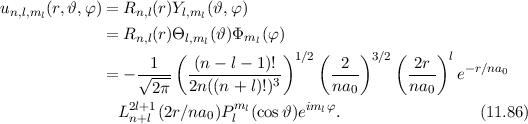
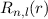 nur für Potentiale
nur für Potentiale
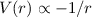 gelten. Die Funktionen
gelten. Die Funktionen 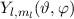 gelten hingegen für beliebige
kugelsymmetrische Potentiale
gelten hingegen für beliebige
kugelsymmetrische Potentiale 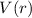 .
.
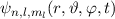 zu
zu
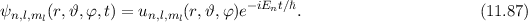
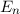 des Wasserstoffs sind gegeben durch
des Wasserstoffs sind gegeben durch 
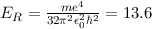 eV die Rydberg-Energie bezeichnet.
eV die Rydberg-Energie bezeichnet.
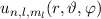 werden durch die Hauptquantenzahl
werden durch die Hauptquantenzahl 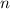 ,
die Bahndrehimpulsquantenzahl
,
die Bahndrehimpulsquantenzahl 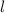 und die magnetische Quantenzahl
und die magnetische Quantenzahl 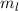 beschrieben. Die Energiewerte
beschrieben. Die Energiewerte 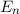 werden durch die Hauptquantenzahl
werden durch die Hauptquantenzahl 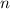 charakterisiert. Dabei gilt
charakterisiert. Dabei gilt 
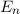 gehören jeweils
gehören jeweils 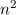 Eigenfunktionen,
d.h. die Energiewerte
Eigenfunktionen,
d.h. die Energiewerte 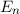 sind
sind 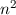 -fach entartet.
-fach entartet.
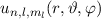 des Hamilton-Operators
des Hamilton-Operators 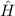 bilden ein
Orthogonalsystem
bilden ein
Orthogonalsystem 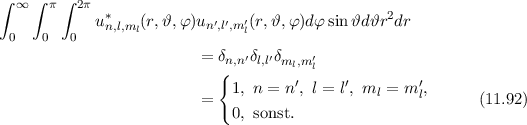
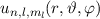 des Hamilton-Operators
des Hamilton-Operators 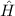 sind
gleichzeitig Eigenfunktionen der Operatoren
sind
gleichzeitig Eigenfunktionen der Operatoren 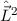 und
und 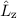 . Die entsprechenden
Eigenwertgleichungen lauten
. Die entsprechenden
Eigenwertgleichungen lauten 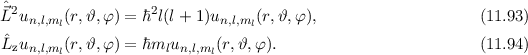
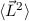 und der z-Komponente des Bahndrehimpulses
und der z-Komponente des Bahndrehimpulses 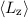 eines Teilchen, das sich in einem kugelsymmetrischen Potential
eines Teilchen, das sich in einem kugelsymmetrischen Potential 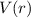 bewegt, nur die diskreten Werte
bewegt, nur die diskreten Werte 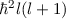 bzw.
bzw. 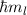 an. Damit ist der
Betrag
an. Damit ist der
Betrag 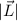 und die z-Komponente
und die z-Komponente 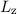 des Bahndrehimpulses durch die
Quantenzahlen
des Bahndrehimpulses durch die
Quantenzahlen 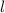 und
und 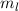 bestimmt. Die x- und y-Komponente sind
unbestimmbar.
bestimmt. Die x- und y-Komponente sind
unbestimmbar.
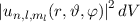 das Elektron im
Volumenelement
das Elektron im
Volumenelement 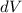 am Ort
am Ort 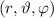 anzutreffen ist gegeben durch
anzutreffen ist gegeben durch
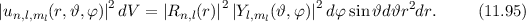
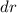 in
einem Abstand
in
einem Abstand  vom Ursprung (Kern) zu finden, ist gegeben durch
vom Ursprung (Kern) zu finden, ist gegeben durch
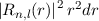 .
.