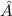 und
und 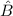 und einen beliebigen Zustand
und einen beliebigen Zustand 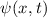 ist gegeben
durch
ist gegeben
durch
Die allgemeine Heisenbergsche Unschärferelation für zwei beliebige hermitesche
Operatoren 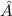 und
und 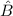 und einen beliebigen Zustand
und einen beliebigen Zustand 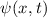 ist gegeben
durch
ist gegeben
durch
Wir leiten nun diese allgemeine Formulierung der Heisenbergschen Unschär-ferelation ausgehend von der sogenannten Schwarzschen Ungleichung her und zeigen anschliessend, dass die Unschärferelation (9.37) für Ort und Impuls als Spezialfall aus (B.1) folgt.
Für zwei beliebige Wellenfunktionen 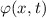 und
und 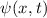 gilt
gilt
Beweis:
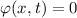 ist die Ungleichung (B.2) erfüllt.
ist die Ungleichung (B.2) erfüllt.
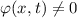 wählen wir den Ansatz
wählen wir den Ansatz wobei 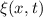 folgende Eigenschaft besitzt
folgende Eigenschaft besitzt
Damit ergibt sich
Daraus folgt für die Konstante 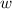 der folgende Ausdruck
der folgende Ausdruck
Mit (B.3), (B.4) und (B.6) erhalten wir schlussendlich

Wir zeigen nun unter Benützung der Schwarzschen Ungleichung (B.2) die Richtigkeit von (B.1).
Es seien 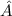 und
und 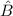 zwei beliebige hermitesche Operatoren und
zwei beliebige hermitesche Operatoren und 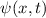 ein
beliebiger Zustand. Nach Definition 9.4 ist das Unschärfeprodukt
ein
beliebiger Zustand. Nach Definition 9.4 ist das Unschärfeprodukt 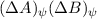 gegeben durch
gegeben durch
Wir führen die beiden hermiteschen Operatoren
ein, womit das Unschärfeprodukt 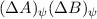 geschrieben werden kann
als
geschrieben werden kann
als
Gleichzeitig gilt aufgrund der Schwarzschen Ungleichung (B.2)
Diese Ungleichung können wir auch schreiben in der Form
Unter Ausnützung der Hermitezität der Operatoren 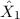 und
und 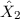 ergibt
sich
ergibt
sich
Der Vergleich mit (B.11) zeigt, dass die linke Seite dieser Ungleichung dem
Quadrat des Unschärfeprodukts 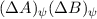 entspricht. Daher ergibt
sich
entspricht. Daher ergibt
sich
Wir führen nun den Antikommutator 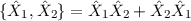 ein und schreiben
damit das Produkt
ein und schreiben
damit das Produkt 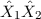 in der Form
in der Form
Einsetzen in die rechte Seite der Ungleichung (B.15) ergibt
Einsetzen in (B.15) liefert
Der Erwartungswert des Antikommutators ist reell und derjenige des Kommutators rein imaginär. Aus diesem Grund können wir schreiben
Wir setzen nun als nächstes die Definitionen (B.9) und (B.10) in den Kommutator
![ˆ ˆ
[X1,X2 ]](PhysikIV6355x.png) ein und erhalten
ein und erhalten
Einsetzen in (B.19) ergibt nun in Übereinstimmung mit (B.1) das folgende Resultat
Wie zu Beginn erwähnt, zeigen wir zum Abschluss, dass die Formulierung (9.37) als
Spezialfall aus (B.1) folgt. Es sei also 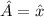 und
und 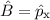 . Einsetzen in (B.1)
ergibt mit (9.85)
. Einsetzen in (B.1)
ergibt mit (9.85)
D.h. es folgt in Übereinstimmung mit (9.37)