Nur eine kleine Anzahl von Elementen existiert natürlich in Form von einzelnen
Atomen. Die meisten Elemente liegen in gebundener Form als einzelne Moleküle in
Flüssigkeiten oder in Festkörpern vor. Ein Molekül ist definiert als eine Verbindung
von zwei oder mehr Atomen zu einer Einheit. Um genau zu sein ist es die kleinste
Einheit einer chemischen Verbindung, die noch deren Eigenschaften aufweist. Der
Begriff Molekül selber kommt aus dem Lateinischen und bedeutet kleine Masse.
Im Allgemeinen gibt es sehr viele Kombinationsmöglichkeiten von Atomen
zu Molekülen. Dieser Tatsache verdanken wir übrigens unseren Reichtum
an Stoffen in unserer Welt. Beispiele von einfachsten Molekülen sind das
Wasserstoffmolekül H , das Stickstoffmolekül N
, das Stickstoffmolekül N und das Sauerstoffmolekül O
und das Sauerstoffmolekül O .
Da diese Moleküle aus zwei gleichen Atomen zusammengesetzt sind, werden
sie als homonuklear bezeichnet. Zweiatomige und heteronukleare (aus zwei
verschiedenen Atomen zusammengesetzte) Moleküle wären zum Beispiel
Lithiumfluorid LiF, Salzsäure HCl oder Kupferoxid CuO. In diesem Kapitel
beschäftigen wir uns mit der Beschreibung der Bildung und der Eigenschaften von
Molekülen.
.
Da diese Moleküle aus zwei gleichen Atomen zusammengesetzt sind, werden
sie als homonuklear bezeichnet. Zweiatomige und heteronukleare (aus zwei
verschiedenen Atomen zusammengesetzte) Moleküle wären zum Beispiel
Lithiumfluorid LiF, Salzsäure HCl oder Kupferoxid CuO. In diesem Kapitel
beschäftigen wir uns mit der Beschreibung der Bildung und der Eigenschaften von
Molekülen.
Im Allgemeinen werden Moleküle dann gebildet, wenn die Gesamtenergie bei ihrer
Bildung aus einzelnen Atomen gesenkt wird, d.h. die Summe der Energien der
einzelnen, getrennten Atome muss grösser sein als die Gesamtenergie des gebildeten
Moleküls. Grundsätzlich gibt es zwei Typen von Bindungen zwischen Molekülen.
Einerseits existiert die kovalente Bindung, auch homöopolare Bindung genannt, und
andererseits die Ionenbindung, auch heteropolare Bindung genannt. Es sei bemerkt,
dass die Erklärung des Zustandekommens beider Bindungen nur mit Hilfe der
Quantenmechanik möglich ist.
Die kovalente Bindung tritt bei Bindungen zwischen Nichtmetallen auf. Das
Zustandekommen der Bindung ist sich so vorzustellen, dass zwischen zwei Atomen,
die ein Molekül bilden, eine anziehende Kraft wirkt, die durch Elektronen vermittelt
wird, welche sich mit hoher Wahrscheinlichkeit zwischen den beiden Atomen
aufhalten. Anders ausgedrückt, die beiden Atome werden durch Elektronen
zusammengehalten, welche gleichzeitig an beide Atome gebunden sind bzw. zwischen
den beiden Atomen hin und her springen.
Ein Beispiel für ein kovalent gebundenes Molekül ist das einfachste existierende
Molekül, das Wasserstoffmolekülion H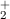 , welches aus zwei Wasserstoffkernen
(Protonen) und einem Elektron besteht. Die Bindung lässt sich so vorstellen, dass das
Elektron die beiden Protonen zusammenhält, indem es zwischen ihnen hin und her
springt. Oder quantenmechanisch ausgedrückt: Zwischen den Wellenfunktionen, die
den Aufenthalt des Elektrons beim einen oder anderen Proton beschreiben, kommt es
zu einer positiven Interferenz, wodurch die Aufenthaltswahrscheinlichkeit des
Elektrons zwischen den beiden beiden Protonen erhöht wird und ein bindender
Zustand entsteht. Auf das Wasserstoffmolekülion H
, welches aus zwei Wasserstoffkernen
(Protonen) und einem Elektron besteht. Die Bindung lässt sich so vorstellen, dass das
Elektron die beiden Protonen zusammenhält, indem es zwischen ihnen hin und her
springt. Oder quantenmechanisch ausgedrückt: Zwischen den Wellenfunktionen, die
den Aufenthalt des Elektrons beim einen oder anderen Proton beschreiben, kommt es
zu einer positiven Interferenz, wodurch die Aufenthaltswahrscheinlichkeit des
Elektrons zwischen den beiden beiden Protonen erhöht wird und ein bindender
Zustand entsteht. Auf das Wasserstoffmolekülion H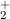 gehen wir in Abschnitt 17.2
noch ausführlicher ein.
gehen wir in Abschnitt 17.2
noch ausführlicher ein.
Es sei an dieser Stelle bemerkt, dass (kovalente) Bindungen nicht gebildet
werden, wenn das Pauli-Prinzip verbietet, dass Elektronen sich in einem
gemeinsamen Quantenzustand aufhalten oder wenn das Pauli-Prinzip nur erfüllt
werden kann, indem Elektronen sich in höher angeregten Zuständen des Atoms
befinden.
Ionenbindungen treten auf, wenn ein Metall und ein Nichtmetall eine Bindung
eingehen. Das Zustandekommen der Bindung ist sich so vorzustellen, dass Elektronen
des einen Atoms auf das andere Atom übergehen und somit positiv und negativ
geladenen Ionen entstehen, zwischen denen eine anziehende Coulomb-Kraft wirkt. Es
stellt sich natürlich noch die Frage, wieso Elektronen vom einen Atom zum anderen
Atom übergehen. Diese Frage kann nur mit Hilfe der Quantenmechanik beantwortet
werden, die besagt, dass es für Elektronen energetisch günstiger sein kann eine nur
teilweise gefüllte Schale des einen Atoms zu verlassen und dafür eine Schale des
anderen Atoms ganz zu füllen. In anderen Worten: Elektronen streben zu
Edelgaskonfigurationen.
Das wahrscheinlich prominenteste Beispiel für eine Ionenbindung ist Kochsalz (NaCl).
Diese Bindung kommt zustande, indem ein Elektron des Na-Atoms zum Cl-Atom
übergeht. Zwischen dem positiv geladenen Na -Ion und dem negativ geladenen
Cl
-Ion und dem negativ geladenen
Cl -Ion herrscht folglich eine elektrische Anziehungskraft und es kommt zur
Bildung des NaCl-Moleküls.
-Ion herrscht folglich eine elektrische Anziehungskraft und es kommt zur
Bildung des NaCl-Moleküls.
Wie bereits erwähnt, ist das Wasserstoffmolekülion H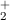 das einfachste
existierende Molekül. Aus diesem Grund eignet es sich sehr gut zur
Illustration des Zustandekommens eines Moleküls (mittels kovalenter
Bindung).
das einfachste
existierende Molekül. Aus diesem Grund eignet es sich sehr gut zur
Illustration des Zustandekommens eines Moleküls (mittels kovalenter
Bindung).
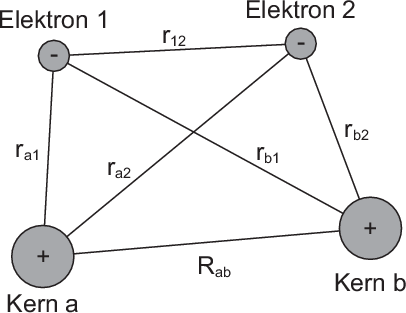
Das Wasserstoffmolekülion wird als gebundener Zustand bei Gasentladungen
in einer Wasserstoffatmosphäre beobachtet. In einer solchen Gasentladung
wird dem Wasserstoffmolekül ein Elektron entrissen. Demzufolge besteht ein
Wasserstoffmolekülion aus zwei Wasserstoffkernen (Protonen) und einem Elektron
(siehe Abb. 17.1).
Wir stellen uns nun die Bildung des Moleküls so vor, dass zuerst die beiden Kerne
weit von einander entfernt sind und sich dann langsam näher kommen. In der
Startposition, wo die Kerne weit auseinander sind, ist das Elektron entweder um den
einen oder den anderen Kern lokalisiert. Die Wellenfunktion des Elektrons entspricht
also derjenigen des Wasserstoffgrundzustands 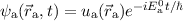 oder
oder
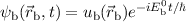 , wobei
, wobei
Zudem lösen die Wellenfunktionen 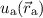 und
und 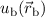 die zeitunabhängige
Schrödinger-Gleichung
die zeitunabhängige
Schrödinger-Gleichung
wobei für die Energiewerte 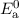 und
und 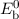 gilt
gilt 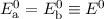 .
.
Wir bringen nun die Kerne näher zusammen. In diesem Fall spürt das Elektron, das
zuvor um eines der beiden Kerne lokalisiert war, die Anziehung beider Kerne. Die
Wellenfunktion 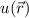 im gebundenen Zustand erfüllt dementsprechend die zeitunabhängige
Schrödinger-Gleichung
im gebundenen Zustand erfüllt dementsprechend die zeitunabhängige
Schrödinger-Gleichung
Das Ziel ist es nun die Wellenfunktion 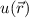 und die Energie
und die Energie 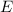 für das Elektron zu
bestimmen. Wie in Abschnitt 17.1.1 erwähnt, können wir das Zustandekommen
der Bindung beim Wasserstoffmolekülion so vorstellen, dass das Elektron
die beiden Protonen zusammenhält, indem es zwischen ihnen hin und her
springt. Aus diesem Grund wählen wir als Ansatz für die Wellenfunktion
für das Elektron zu
bestimmen. Wie in Abschnitt 17.1.1 erwähnt, können wir das Zustandekommen
der Bindung beim Wasserstoffmolekülion so vorstellen, dass das Elektron
die beiden Protonen zusammenhält, indem es zwischen ihnen hin und her
springt. Aus diesem Grund wählen wir als Ansatz für die Wellenfunktion 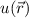 eine Linearkombination der beiden Wellenfunktionen
eine Linearkombination der beiden Wellenfunktionen 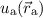 und
und 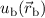 ,
d.h.
,
d.h.
wobei 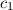 und
und 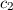 zwei noch zu bestimmende Koeffizienten sind. Einsetzen in (17.5)
liefert
zwei noch zu bestimmende Koeffizienten sind. Einsetzen in (17.5)
liefert
wobei wir die beiden Hamiltonoperatoren 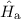 und
und 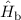 eingeführt haben. Wir
können nun diese Gleichung mit Hilfe der Schrödinger-Gleichungen (17.3) und (17.4)
vereinfachen. Es ergibt sich
eingeführt haben. Wir
können nun diese Gleichung mit Hilfe der Schrödinger-Gleichungen (17.3) und (17.4)
vereinfachen. Es ergibt sich
wobei wir den Energieunterschied zwischen der Grundzustandsenergie 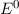 und der
Energie des Elektrons im gebundenen Zustand
und der
Energie des Elektrons im gebundenen Zustand 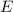 mit
mit 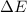 bezeichnet haben. Wir
multiplizieren nun diese Gleichung mit
bezeichnet haben. Wir
multiplizieren nun diese Gleichung mit 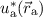 und integrieren über die
Ortskoordinate des Elektrons
und integrieren über die
Ortskoordinate des Elektrons 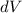
wobei wir für die verschiedenen Integrale die Konstanten 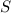 ,
, 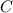 und
und 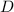 eingeführt
haben. Mit diesen Konstanten lässt sich diese Gleichung in der einfachen
Form
eingeführt
haben. Mit diesen Konstanten lässt sich diese Gleichung in der einfachen
Form
schreiben. Analog multiplizieren wir (17.8) mit 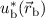 und integrieren wiederum
über die Ortskoordinate des Elektrons
und integrieren wiederum
über die Ortskoordinate des Elektrons 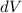 . Es ergibt sich
. Es ergibt sich
wobei wir aus Symmetriegründen die Integrale durch die selben Konstanten S, C, und
D wie zuvor ersetzen können und somit die Gleichung in der Form
schreiben können. Wir haben nun mit den Gleichungen (17.10) und (17.12)
zwei Gleichungen für die beiden Koeffizienten 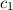 und
und 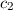 gefunden. Dieses
Gleichungssystem lässt sich in Matrixschreibweise darstellen
gefunden. Dieses
Gleichungssystem lässt sich in Matrixschreibweise darstellen
Ein Gleichungssystem dieser Art hat nur dann eine nichttriviale Lösung, wenn die
Determinante der Matrix verschwindet, d.h. wenn gilt
und somit
Einsetzen in (17.13) ergibt für die Koeffizienten 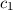 und
und 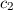 die Lösungen
die Lösungen
Daraus erhalten wir für die Wellenfunktion 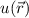 ein antisymmetrische
ein antisymmetrische 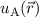 und eine symmetrische
und eine symmetrische
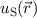 Lösung
Lösung
Die entsprechenden Energiewerte 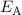 und
und 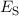 lauten
lauten
Nun stellt sich die Frage, ob beide dieser Zustände realisiert werden, nur einer der
beiden oder keiner, d.h. kurz gesagt, ob überhaupt eine Bindung zustande kommt.
Die Antwort auf diese Frage ergibt sich aus der Berechnung der Bindungsenergie,
d.h. aus dem Vergleich der Gesamtenergie bei weit auseinander liegenden Kernen mit
der Gesamtenergie bei nahe beieinander liegenden Kernen. Nur wenn die
Bindungsenergie bei einem bestimmten Abstand der Kerne negativ ist, kommt es zur
Bindung.
Die Gesamtenergie 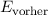 bei weit auseinander liegenden Kernen entspricht der
Grundzustandsenergie
bei weit auseinander liegenden Kernen entspricht der
Grundzustandsenergie 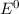 des Wasserstoffatoms. Die Gesamtenergie
des Wasserstoffatoms. Die Gesamtenergie 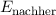 bei
nahe beieinander liegenden Kernen ergibt sich aus der Summe der Energie des
Elektrons
bei
nahe beieinander liegenden Kernen ergibt sich aus der Summe der Energie des
Elektrons 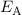 oder
oder 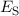 und der Coulombschen Abstossungsenergie
und der Coulombschen Abstossungsenergie 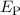 zwischen
den Protonen
zwischen
den Protonen
Mit (17.20) und (17.21) folgt somit für die Bindungsenergie 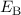 des
Wasserstoffmolekülions
des
Wasserstoffmolekülions
Die Darstellung der Bindungsenergie 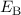 in Abhängigkeit des Abstands
in Abhängigkeit des Abstands 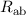 zwischen den Kernen (siehe Abb. 17.2) zeigt, dass im antisymmetrischen Zustand die
Bindungsenergie stets positiv ist und daher keine Bindung eintritt. Dieser Zustand
wird daher antibindender Zustand genannt. Umgekehrt wird für den symmetrischen
Zustand die Bindungsenergie in einem bestimmten Abstandsbereich negativ und es
kommt somit zur Bindung. Der symmetrische Zustand wird daher bindender Zustand
genannt. Nach unserem Modell beträgt die Bindungsenergie
zwischen den Kernen (siehe Abb. 17.2) zeigt, dass im antisymmetrischen Zustand die
Bindungsenergie stets positiv ist und daher keine Bindung eintritt. Dieser Zustand
wird daher antibindender Zustand genannt. Umgekehrt wird für den symmetrischen
Zustand die Bindungsenergie in einem bestimmten Abstandsbereich negativ und es
kommt somit zur Bindung. Der symmetrische Zustand wird daher bindender Zustand
genannt. Nach unserem Modell beträgt die Bindungsenergie 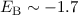 eV
bei einem Abstand
eV
bei einem Abstand 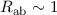 Å zwischen den Kernen (siehe Abb. 17.2).
Å zwischen den Kernen (siehe Abb. 17.2).
Um uns das Zustandekommen einer Bindung im symmetrischen (bindenden)
Zustand bzw. das Nichtzustandekommen einer Bindung im antisymmetrischen
(antibindenden) Zustand noch besser vorzustellen, werfen wir einen Blick auf die
entsprechenden Wellenfunktionen 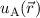 und
und 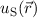 . Im symmetrischen Zustand
(siehe Abb. 17.3(a)) ist aufgrund der Überlappung der Wellenfunktionen
. Im symmetrischen Zustand
(siehe Abb. 17.3(a)) ist aufgrund der Überlappung der Wellenfunktionen 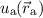 und
und 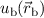 die Aufenthaltswahrscheinlichkeit für das Elektron zwischen
den beiden Kernen erhöht. Folglich hält sich das Elektron häufig zwischen
den Kernen auf, wo es die Anziehungskraft beider Kerne spürt. Dadurch
wird die potentielle Energie des Gesamtsystems gesenkt, was zur Bindung
führt. Im antisymmetrischen Zustand (siehe Abb. 17.3(b)) ist hingegen die
Aufenthaltswahrscheinlichkeit zwischen den Kernen klein, in der Mitte sogar null.
Das bedeutet, dass sich das Elektron selten bis gar nie zwischen den Kernen
aufhält und meistens nur die Anziehungskraft eines Kerns zu spüren bekommt.
die Aufenthaltswahrscheinlichkeit für das Elektron zwischen
den beiden Kernen erhöht. Folglich hält sich das Elektron häufig zwischen
den Kernen auf, wo es die Anziehungskraft beider Kerne spürt. Dadurch
wird die potentielle Energie des Gesamtsystems gesenkt, was zur Bindung
führt. Im antisymmetrischen Zustand (siehe Abb. 17.3(b)) ist hingegen die
Aufenthaltswahrscheinlichkeit zwischen den Kernen klein, in der Mitte sogar null.
Das bedeutet, dass sich das Elektron selten bis gar nie zwischen den Kernen
aufhält und meistens nur die Anziehungskraft eines Kerns zu spüren bekommt.
Zum Abschluss der Betrachtung des Wasserstoffmolekülions vergleichen wir die Werte
für die Bindungsenergie 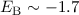 eV und den Abstand
eV und den Abstand 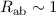 Å zwischen
den Kernen aus unserem Modell mit den experimentell bestimmten Werten
Å zwischen
den Kernen aus unserem Modell mit den experimentell bestimmten Werten
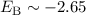 eV und
eV und 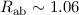 Å . Es ist zu erkennen, dass die Abweichung
der Werte relativ gross ist. Trotzdem haben wir mit unserem Modell eine
gute Vorstellung erhalten wie es zur Bindung beim Wasserstoffmolekülion
kommt.
Å . Es ist zu erkennen, dass die Abweichung
der Werte relativ gross ist. Trotzdem haben wir mit unserem Modell eine
gute Vorstellung erhalten wie es zur Bindung beim Wasserstoffmolekülion
kommt.
Nach dem Wasserstoffmolekülion erweitern wir unsere Betrachtung auf Moleküle mit
mehreren Elektronen. Das einfachste solche Molekül ist das Wasserstoffmolekül,
welches aus zwei Wasserstoffkernen (Protonen) und zwei Elektronen besteht (siehe
Abb. 17.4).
Die Wellenfunktion 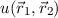 dieses Zweielektronensystems erfüllt die
Schrödinger-Gleichung
dieses Zweielektronensystems erfüllt die
Schrödinger-Gleichung
wobei der Hamiltonoperator 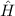 gegeben ist durch
gegeben ist durch
Das Ziel ist es nun wie beim Wasserstoffmolekülion die Wellenfunktion 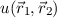 und
die Energie
und
die Energie 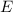 zu bestimmen. Dazu verwenden wir das Lösungsverfahren von
Heitler-London, welches nach Walter Heitler und Fritz London benannt ist und auf
dem sogenannten Variationsprinzip beruht.
zu bestimmen. Dazu verwenden wir das Lösungsverfahren von
Heitler-London, welches nach Walter Heitler und Fritz London benannt ist und auf
dem sogenannten Variationsprinzip beruht.
Multiplikation der Schrödinger-Gleichung (17.24) mit 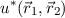 und Integration
über die Ortskoordinaten
und Integration
über die Ortskoordinaten 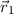 und
und 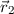 ergibt für die Energiewerte
ergibt für die Energiewerte 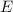 den
Ausdruck
den
Ausdruck
Das Variationsprinzip besagt nun, dass wenn anstelle der Lösung der
Schrödinger-Gleichung 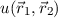 eine andere Funktion eingesetzt wird, man eine
angenäherte Lösung für die Energiewerte
eine andere Funktion eingesetzt wird, man eine
angenäherte Lösung für die Energiewerte 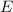 erhält oder genauer gesagt eine obere
Grenze.
erhält oder genauer gesagt eine obere
Grenze.
Da wir nun beim Wasserstoffmolekül im Vergleich zum Wasserstoffmolekülion zwei
Elektronen anstelle von einem Elektron vorliegen haben, müssen wir beim
Aufstellen eines Ansatzes für die Wellenfunktion 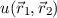 das Pauli-Prinzip
berücksichtigen, d.h. die Gesamtwellenfunktion inklusive Spins der Elektronen des
Wasserstoffmoleküls muss antisymmetrisch sein. Die erste Möglichkeit diese
Bedingung zu erfüllen, ergibt sich mit einer symmetrischen Ortswellenfunktion und
einer antisymmetrischen Spinwellenfunktion
das Pauli-Prinzip
berücksichtigen, d.h. die Gesamtwellenfunktion inklusive Spins der Elektronen des
Wasserstoffmoleküls muss antisymmetrisch sein. Die erste Möglichkeit diese
Bedingung zu erfüllen, ergibt sich mit einer symmetrischen Ortswellenfunktion und
einer antisymmetrischen Spinwellenfunktion
wobei die symmetrische Ortswellenfunktion 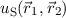 nach (16.13) gegeben ist
durch
nach (16.13) gegeben ist
durch
und die antisymmetrische Spinwellenfunktion 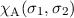 durch
durch
Die zweite Möglichkeit eine antisymmetrische Gesamtwellenfunktion zu konstruieren,
ergibt sich mit einer antisymmetrischen Ortswellenfunktion und einer symmetrischen
Spinwellenfunktion
wobei die antisymmetrische Ortswellenfunktion 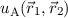 nach (16.14) gegeben ist
durch
nach (16.14) gegeben ist
durch
und die symmetrische Spinwellenfunktion 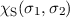 durch
durch
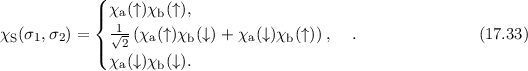
Nach Lösungsverfahren von Heitler-London sind nun diese beiden Wellenfunktionen
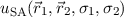 und
und 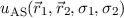 als Ansatz für die Wellenfunktion
als Ansatz für die Wellenfunktion
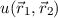 zu wählen, diese in (17.26) einzusetzen und somit eine im Sinne des
Variationsprinzips angenäherte Lösung für die Energiewerte des Wasserstoffmoleküls
zu erhalten. Wir verzichten an dieser Stelle auf diese Rechnung und betrachten gleich
die Lösung für die Bindungsenergie
zu wählen, diese in (17.26) einzusetzen und somit eine im Sinne des
Variationsprinzips angenäherte Lösung für die Energiewerte des Wasserstoffmoleküls
zu erhalten. Wir verzichten an dieser Stelle auf diese Rechnung und betrachten gleich
die Lösung für die Bindungsenergie 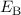 für die beiden Fälle (siehe Abb. 17.5).
Wie im Fall des Wasserstoffmolekülions führen im Wasserstoffmolekül die
Wellenfunktionen mit symmetrischer Ortswellenfunktion zu bindenden Zuständen,
wohingegen die Wellenfunktionen mit antisymmetrischer Ortswellenfunktion zu
antibindenden Zuständen führen. Nach unserem Modell beträgt die Bindungsenergie
für die beiden Fälle (siehe Abb. 17.5).
Wie im Fall des Wasserstoffmolekülions führen im Wasserstoffmolekül die
Wellenfunktionen mit symmetrischer Ortswellenfunktion zu bindenden Zuständen,
wohingegen die Wellenfunktionen mit antisymmetrischer Ortswellenfunktion zu
antibindenden Zuständen führen. Nach unserem Modell beträgt die Bindungsenergie
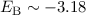 eV bei einem Abstand
eV bei einem Abstand 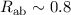 Å zwischen den Kernen.
Wiederum sind die Abweichungen zu den experimentell bestimmten Werten
Å zwischen den Kernen.
Wiederum sind die Abweichungen zu den experimentell bestimmten Werten
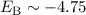 eV und
eV und 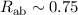 Å relativ gross. Das bedeutet, dass die
Wellenfunktion nach dem Heitler-London-Modell noch relativ ungenau sind und
zur Verbesserung des Modells noch weitere Effekte zu berücksichtigen sind.
Å relativ gross. Das bedeutet, dass die
Wellenfunktion nach dem Heitler-London-Modell noch relativ ungenau sind und
zur Verbesserung des Modells noch weitere Effekte zu berücksichtigen sind.
An dieser Stelle sei noch bemerkt, dass - wie zu erwarten - die Bindungsenergie beim
Wasserstoffmolekül stärker als beim Wasserstoffmolekülion ist, da sich zwei
Elektronen für die Bindung zwischen den Kernen verantwortlich zeigen.
Die Beschreibung von komplexeren Molekülen als das Wasserstoffmolekülion
oder das Wasserstoffmolekül ist allgemein eine sehr schwierige Aufgabe.
Hilfreich ist nur die Tatsache, dass es häufig ausreicht die Wechselwirkung der
Elektronen in den äusseren Schalen (Valenzelektronen) der beteiligten Atome zu
untersuchen. Der Grund dafür liegt darin, dass Elektronen in den inneren
Schalen aufgrund ihrer starken Bindung an den Atomkern nur schwach zu
Atom-Atom-Wechselwirkungen beitragen. Zudem bestätigen Röntgen-Spektren diese
Feststellung.
Der Grund wieso gewisse Moleküle wie das Wasserstoffmolekül H oder das
Wassermolekül H
oder das
Wassermolekül H O gebildet werden und andere Moleküle wie das Heliummolekül
He
O gebildet werden und andere Moleküle wie das Heliummolekül
He nicht, liegt im Wesentlichen beim Pauli-Prinzip. Zum Beispiel hat
das Heliumatom im Grundzustand zwei Elektronen im
nicht, liegt im Wesentlichen beim Pauli-Prinzip. Zum Beispiel hat
das Heliumatom im Grundzustand zwei Elektronen im 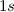 -Zustand mit
unterschiedlichem Spin. Wenn es nun mit einem anderen Heliumatom zusammen
kommt, wird jedes Heliumatom einen Teil der Zeit zwei Elektronen mit dem selben
Spin haben. Nach dem Pauli-Prinzip ist dies jedoch verboten und deshalb existiert
das Heliummolekül He
-Zustand mit
unterschiedlichem Spin. Wenn es nun mit einem anderen Heliumatom zusammen
kommt, wird jedes Heliumatom einen Teil der Zeit zwei Elektronen mit dem selben
Spin haben. Nach dem Pauli-Prinzip ist dies jedoch verboten und deshalb existiert
das Heliummolekül He nicht.
nicht.
Wir werfen nun nochmals einen Blick auf das Zustandekommen einer (kovalenten)
Bindung zwischen zwei Atomen. Quantenmechanisch gesehen überlappen beim
Zusammenkommen von zwei Atomen ihre Wellenfunktionen. Wird durch diesen
Überlapp die Wahrscheinlichkeitsdichte der Elektronen zwischen den beteiligten
Atomen erhöht, führt dies zu anziehenden Kräften und schliesslich zu einer
(kovalenten) Bindung. Die dabei involvierten Elektronen können jedoch
Wahrscheinlichkeitsdichten aufweisen, die sich von denen bei isolierten Atomen
unterscheiden. Folgende s- und p-Zustände sind wichtig bei der Bildung von
Bindungen bei Molekülen (siehe Abb. 17.6):
 -Zustände (
-Zustände (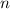 = 1, 2, 3, ...,
= 1, 2, 3, ..., 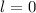 ,
, 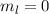 ):
):
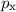 -Zustände (
-Zustände (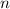 = 2, 3, 4, ...,
= 2, 3, 4, ..., 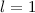 ,
, 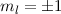 ):
):
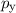 -Zustände (
-Zustände (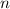 = 2, 3, 4, ...,
= 2, 3, 4, ..., 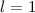 ,
, 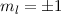 ):
):
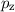 -Zustände (
-Zustände (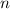 = 2, 3, 4, ...,
= 2, 3, 4, ..., 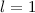 ,
, 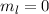 ):
):
Molekülzustände werden gemäss ihrer Gesamtdrehimpulsquantenzahl 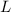 (Gesamtdrehimpuls entlang der Bindungsachse, d.h. z-Achse) mit einem griechischen
Buchstaben versehen:
(Gesamtdrehimpuls entlang der Bindungsachse, d.h. z-Achse) mit einem griechischen
Buchstaben versehen:
Beim Wasserstoffmolekül liegt z.B. eine 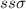 -Bindung vor. Allgemein bilden
-Bindung vor. Allgemein bilden
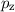 Zustände
Zustände 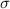 -Bindungen,
-Bindungen, 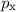 - und
- und 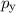 -Zustände
-Zustände 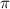 -Bindungen. Es
können auch Bindungen aus Zuständen, die zu unterschiedlichen Drehimpulsen
gehören, gebildet werden. Ein Beispiel ist das Wassermolekül. Die zwei einfach
besetzten
-Bindungen. Es
können auch Bindungen aus Zuständen, die zu unterschiedlichen Drehimpulsen
gehören, gebildet werden. Ein Beispiel ist das Wassermolekül. Die zwei einfach
besetzten 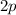 -Zustände des Sauerstoffatoms kommen mit den
-Zustände des Sauerstoffatoms kommen mit den 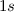 -Zuständen
der Wasserstoffatome zusammen und bilden jeweils eine
-Zuständen
der Wasserstoffatome zusammen und bilden jeweils eine 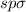 -Bindung.
Dabei bewirkt die gegenseitige Abstossung zwischen den Wasserstoffatomen
eine Vergrösserung des Winkels zwischen den Bindungsachsen von 90
-Bindung.
Dabei bewirkt die gegenseitige Abstossung zwischen den Wasserstoffatomen
eine Vergrösserung des Winkels zwischen den Bindungsachsen von 90 zu
104.5
zu
104.5 .
.
Diese Erklärung des Zustandekommens einer Bindung beim Wassermolekül kann
nicht bei allen Molekülen angewendet werden wie das Beispiel von Methan CH zeigt. Man würde nämlich erwarten, dass das Kohlenstoffatom mit einer
Elektronenkonfiguration
zeigt. Man würde nämlich erwarten, dass das Kohlenstoffatom mit einer
Elektronenkonfiguration 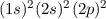 mit zwei Wasserstoffatomen ein CH
mit zwei Wasserstoffatomen ein CH Molekül mit zwei
Molekül mit zwei 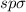 -Bindungen unter einem Bindungswinkel von etwas mehr als
90
-Bindungen unter einem Bindungswinkel von etwas mehr als
90 bildet. In der Natur kommt aber auch das Methan-Molekül CH
bildet. In der Natur kommt aber auch das Methan-Molekül CH vor, das perfekt symmetrisch ist mit vier exakt gleichen C-H-Bindungen. Es
stellt sich jetzt natürlich die Frage, wie ist eine solche Bindung möglich. Die
Antwort ist, dass es beim Kohlenstoffatom zur Bildung von Superpositionen aus
dem
vor, das perfekt symmetrisch ist mit vier exakt gleichen C-H-Bindungen. Es
stellt sich jetzt natürlich die Frage, wie ist eine solche Bindung möglich. Die
Antwort ist, dass es beim Kohlenstoffatom zur Bildung von Superpositionen aus
dem 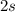 -Zustand und den drei
-Zustand und den drei 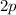 -Zuständen zu vier neuen Zuständen
(
-Zuständen zu vier neuen Zuständen
(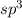 -Zustände) kommt. Dieses Phänomen wird Hybridisierung genannt. Solche
hybridisierten Zustände treten auf, wenn die Bindungsenergien niedriger sind als
die der nicht hybridisierten Zustände. Es sei an dieser Stelle bemerkt, dass
beim Kohlenstoffatom noch zwei weitere Möglichkeiten von hybridisierten
Zuständen vorkommen:
-Zustände) kommt. Dieses Phänomen wird Hybridisierung genannt. Solche
hybridisierten Zustände treten auf, wenn die Bindungsenergien niedriger sind als
die der nicht hybridisierten Zustände. Es sei an dieser Stelle bemerkt, dass
beim Kohlenstoffatom noch zwei weitere Möglichkeiten von hybridisierten
Zuständen vorkommen: 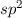 -Zustände (ein Elektron bleibt im
-Zustände (ein Elektron bleibt im 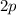 -Zustand,
die übrigen drei besetzen hybridisierte Zustände) und
-Zustand,
die übrigen drei besetzen hybridisierte Zustände) und 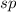 -Zustände (zwei
Elektronen bleiben im
-Zustände (zwei
Elektronen bleiben im 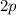 -Zustand, die übrigen zwei besetzen hybridisierte
Zustände).
-Zustand, die übrigen zwei besetzen hybridisierte
Zustände).
Die Gesamtenergie eines Moleküls hängt von seinem elektronischen Zustand, den
Schwingungen der gebundenen Atome gegeneinander und der Rotation des Moleküls
als Ganzes ab. Bei diesen drei Energien bewegen sich die Abstände zwischen
den diskreten Energielevels auf unterschiedlichen Skalen, was sich auch in
Molekülspektren widerspiegelt:
- Der Abstand der Energielevels für die äussersten Elektronen bei Molekülen
liegt bei einigen eV, was Spektrallinien im sichtbares oder UV-Bereich zur
Folge hat.
- Schwingungszustände sind getrennt durch einige 0.1 eV. Übergänge
zwischen diesen Zuständen führen zu Spektrallinien im infraroten Bereich.
- Noch auf einer kleineren Skala bewegen sich die Abstände der
Rotationszustände. Sie liegen im Bereich von einigen meV, was
Spektrallinen im Mikrowellen-Bereich hervorruft.
Molekülspektren sind hilfreich zur Analyse der Struktur von Molekülen. Zum Beispiel
können Bindungslängen und Bindungswinkel aus den Schwingungs- und
Rotationsspektren bestimmt werden
Um eine Idee von Rotationsspektren zu erhalten betrachten wir ein zweiatomiges
Molekül, welches um den Schwerpunkt rotiert (siehe Abb. 17.7).
Das Trägheitsmoment dieses Moleküls um eine Achse durch den Schwerpunkt und
senkrecht zur Verbindungslinie der beiden Atome beträgt
wobei wir im letzten Schritt die reduzierte Masse
eingeführt haben. Folglich entspricht die Rotation eines zweiatomigen Moleküls
der Rotation eines einzigen Teilchens der Masse 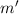 um eine Achse mit
Abstand
um eine Achse mit
Abstand 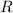 . Der Betrag des Drehimpulses
. Der Betrag des Drehimpulses 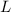 des Moleküls ist gegeben
durch
des Moleküls ist gegeben
durch
wobei 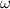 die Winkelgeschwindigkeit ist. Wie immer ist der Drehimpuls quantisiert,
d.h. es gilt
die Winkelgeschwindigkeit ist. Wie immer ist der Drehimpuls quantisiert,
d.h. es gilt
wobei wir die Rotationsquantenzahl 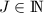 eingeführt haben. Damit ergibt sich für
die Rotationsenergie
eingeführt haben. Damit ergibt sich für
die Rotationsenergie
Die Linien im Spektrum ergeben sich durch Übergänge zwischen den verschiedenen
Energielevels 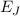 . Für die Übergangsfrequenzen
. Für die Übergangsfrequenzen  gilt
gilt
Jedoch sind wie bei Atomen die Übergänge, die realisiert werden, durch eine
Auswahlregel eingeschränkt
Zudem zeigen ausschliesslich Moleküle mit einem permanenten Dipolmoment
Rotationsspektren, da nur solche Moleküle elektromagnetische Strahlung emittieren
oder absorbieren können. Moleküle ohne permanentes Dipolmoment können
ihren Rotationszustand nur durch Stösse verändern. Beispiele für Moleküle
ohne permanentes Dipolmoment sind Methan CH oder Kohlenstoffdioxid
CO
oder Kohlenstoffdioxid
CO .
.
Nach (17.43) ist die Übergangsfrequenz  proportional zur Rotationsquantenzahl
proportional zur Rotationsquantenzahl
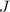 . Aus diesem Grund sind im Spektrum eines Moleküls äquidistante Spektrallinien
zu beobachten.
. Aus diesem Grund sind im Spektrum eines Moleküls äquidistante Spektrallinien
zu beobachten.
Aus der Messung eines Rotationsspektrums kann mit (17.43) das Trägheitsmoment
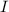 eines Moleküls bestimmt werden. Sind zudem die Massen
eines Moleküls bestimmt werden. Sind zudem die Massen 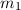 und
und 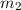 der
beteiligten Atome bekannt, ergibt sich mit (17.38) die Bindungslänge
der
beteiligten Atome bekannt, ergibt sich mit (17.38) die Bindungslänge 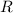 des
Moleküls.
des
Moleküls.
Moleküle können zu Schwingungen entlang ihrer Bindungen angeregt werden. Für
kleine Amplituden sind die Schwingungen eines Moleküls gut durch einen
harmonischen Oszillator beschrieben. Die Schwingungsenergie ist daher nach
Kapitel 10 gegeben durch
wobei wir die Schwingungsquantenzahl  eingeführt haben und nur die Übergänge,
die die Auswahlregel
eingeführt haben und nur die Übergänge,
die die Auswahlregel 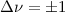 erfüllen, zugelassen sind. In der Realität ist der
Abstand der Energieniveaus der Molekülschwingung nicht äquidistant, sondern
nimmt für hohe Energien ab. Der Grund dafür liegt darin, dass für hohe Energien die
Beschreibung durch den harmonischen Oszillator nicht mehr gerechtfertigt
ist.
erfüllen, zugelassen sind. In der Realität ist der
Abstand der Energieniveaus der Molekülschwingung nicht äquidistant, sondern
nimmt für hohe Energien ab. Der Grund dafür liegt darin, dass für hohe Energien die
Beschreibung durch den harmonischen Oszillator nicht mehr gerechtfertigt
ist.
Mehratomige Moleküle haben verschiedenen Schwingungsmoden. Diese können lokal
in nur einem Teil des Moleküls auftreten oder global im ganzen Molekül.
Insbesondere auch diese Tatsache erlaubt aufgrund von Untersuchungen von
Schwingungsspektren die Bindungsstruktur von Molekülen im Detail zu
untersuchen.
Fluoreszenz und Phosphoreszenz sind zwei Phänomene, welche im Zusammenhang
mit Rotations- und Schwingungsspektren auftreten.
Zur Erklärung von Fluoreszenz betrachten wir ein Molekül, welches durch Absorption
eines Photons angeregt wurde. Der angeregte Zustand kann dann zurück in den
Grundzustand übergehen. Dies kann auf zwei unterschiedlichen Arten geschehen.
Einerseits durch aussenden eines Photons der selben Frequenz oder andererseits kann
das Molekül zuerst Schwingungsenergie in Kollisionen mit anderen Molekülen
verlieren und dann ein Photon mit niedriger Frequenz aussenden. Tritt die zweite
Variante auf, spricht man Fluoreszenz. Das Prinzip von Fluoreszenz kommt
zum Beispiel bei Leuchtstoffröhren oder bei Aufheller in Waschmitteln zur
Anwendung.
Phosphoreszenz tritt auf, wenn ein Molekül von einem Singulett-Grundzustand
in einen angeregten Singulett-Zustand angeregt wird und anschliessend in
Folge von Kollisionen mit anderen Molekülen aus dem Singulett-Zustand in
ein Triplett-Zustand übergeht. Der Triplett-Zustand geht nun aufgrund der
Auswahlregel 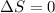 für die Spinquantenzahl sehr unwahrscheinlich in den
Grundzustand zurück und das Molekül verweilt in einem sogenannte metastabilen
Zustand.
Solche Moleküle können daher noch lange nach der Anregung ihre Energie wieder
abgeben. Phosphoreszenz wird zum Beispiel bei Schildern oder Leuchtziffern
eingesetzt.
für die Spinquantenzahl sehr unwahrscheinlich in den
Grundzustand zurück und das Molekül verweilt in einem sogenannte metastabilen
Zustand.
Solche Moleküle können daher noch lange nach der Anregung ihre Energie wieder
abgeben. Phosphoreszenz wird zum Beispiel bei Schildern oder Leuchtziffern
eingesetzt.
- Vorlesungsfolien Frühlingssemester 2008
- A. Beiser, Concepts of Modern Physics, McGraw-Hill, 2003
- H. Haken and H. Wolf, Atom- und Quantenphysik, Einführung in
die experimentellen und theoretischen Grundlagen, Springer, Berlin
Heidelberg New York, 2004.
- H. Haken and H. Wolf, Molekülphysik und Quantenchemie, Einführung
in die experimentellen und theoretischen Grundlagen, Springer, Berlin
Heidelberg New York, 2003.
- F. Schwabl, Quantenmechanik (QM I), Eine Einführung, Springer, Berlin
Heidelberg New York, 2002.
 , das Stickstoffmolekül N
, das Stickstoffmolekül N und das Sauerstoffmolekül O
und das Sauerstoffmolekül O .
Da diese Moleküle aus zwei gleichen Atomen zusammengesetzt sind, werden
sie als homonuklear bezeichnet. Zweiatomige und heteronukleare (aus zwei
verschiedenen Atomen zusammengesetzte) Moleküle wären zum Beispiel
Lithiumfluorid LiF, Salzsäure HCl oder Kupferoxid CuO. In diesem Kapitel
beschäftigen wir uns mit der Beschreibung der Bildung und der Eigenschaften von
Molekülen.
.
Da diese Moleküle aus zwei gleichen Atomen zusammengesetzt sind, werden
sie als homonuklear bezeichnet. Zweiatomige und heteronukleare (aus zwei
verschiedenen Atomen zusammengesetzte) Moleküle wären zum Beispiel
Lithiumfluorid LiF, Salzsäure HCl oder Kupferoxid CuO. In diesem Kapitel
beschäftigen wir uns mit der Beschreibung der Bildung und der Eigenschaften von
Molekülen.
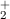 , welches aus zwei Wasserstoffkernen
(Protonen) und einem Elektron besteht. Die Bindung lässt sich so vorstellen, dass das
Elektron die beiden Protonen zusammenhält, indem es zwischen ihnen hin und her
springt. Oder quantenmechanisch ausgedrückt: Zwischen den Wellenfunktionen, die
den Aufenthalt des Elektrons beim einen oder anderen Proton beschreiben, kommt es
zu einer positiven Interferenz, wodurch die Aufenthaltswahrscheinlichkeit des
Elektrons zwischen den beiden beiden Protonen erhöht wird und ein bindender
Zustand entsteht. Auf das Wasserstoffmolekülion H
, welches aus zwei Wasserstoffkernen
(Protonen) und einem Elektron besteht. Die Bindung lässt sich so vorstellen, dass das
Elektron die beiden Protonen zusammenhält, indem es zwischen ihnen hin und her
springt. Oder quantenmechanisch ausgedrückt: Zwischen den Wellenfunktionen, die
den Aufenthalt des Elektrons beim einen oder anderen Proton beschreiben, kommt es
zu einer positiven Interferenz, wodurch die Aufenthaltswahrscheinlichkeit des
Elektrons zwischen den beiden beiden Protonen erhöht wird und ein bindender
Zustand entsteht. Auf das Wasserstoffmolekülion H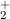 gehen wir in Abschnitt
gehen wir in Abschnitt  -Ion und dem negativ geladenen
Cl
-Ion und dem negativ geladenen
Cl -Ion herrscht folglich eine elektrische Anziehungskraft und es kommt zur
Bildung des NaCl-Moleküls.
-Ion herrscht folglich eine elektrische Anziehungskraft und es kommt zur
Bildung des NaCl-Moleküls.
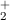 das einfachste
existierende Molekül. Aus diesem Grund eignet es sich sehr gut zur
Illustration des Zustandekommens eines Moleküls (mittels kovalenter
Bindung)
das einfachste
existierende Molekül. Aus diesem Grund eignet es sich sehr gut zur
Illustration des Zustandekommens eines Moleküls (mittels kovalenter
Bindung)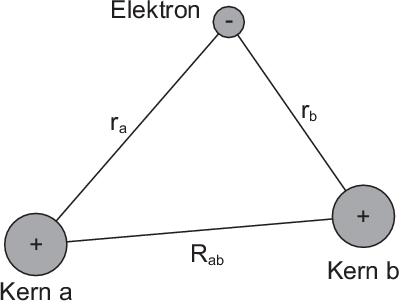
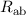 , der Abstand des Elektrons zu den beiden Kernen mit
, der Abstand des Elektrons zu den beiden Kernen mit
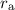 bzw.
bzw. 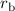 .
.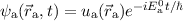 oder
oder
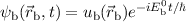 , wobei
, wobei

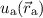 und
und 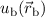 die zeitunabhängige
Schrödinger-Gleichung
die zeitunabhängige
Schrödinger-Gleichung
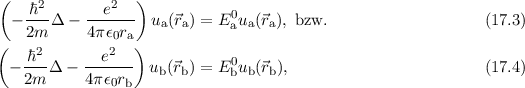
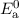 und
und 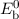 gilt
gilt 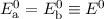 .
.
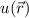 im gebundenen Zustand erfüllt dementsprechend die zeitunabhängige
Schrödinger-Gleichung
im gebundenen Zustand erfüllt dementsprechend die zeitunabhängige
Schrödinger-Gleichung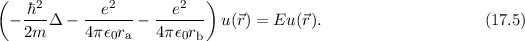
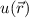 und die Energie
und die Energie 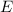 für das Elektron zu
bestimmen. Wie in Abschnitt
für das Elektron zu
bestimmen. Wie in Abschnitt 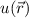 eine Linearkombination der beiden Wellenfunktionen
eine Linearkombination der beiden Wellenfunktionen 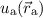 und
und 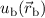 ,
d.h.
,
d.h.

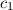 und
und 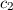 zwei noch zu bestimmende Koeffizienten sind. Einsetzen in (
zwei noch zu bestimmende Koeffizienten sind. Einsetzen in (
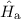 und
und 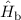 eingeführt haben. Wir
können nun diese Gleichung mit Hilfe der Schrödinger-Gleichungen (
eingeführt haben. Wir
können nun diese Gleichung mit Hilfe der Schrödinger-Gleichungen (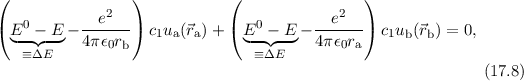
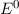 und der
Energie des Elektrons im gebundenen Zustand
und der
Energie des Elektrons im gebundenen Zustand 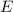 mit
mit 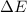 bezeichnet haben. Wir
multiplizieren nun diese Gleichung mit
bezeichnet haben. Wir
multiplizieren nun diese Gleichung mit 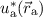 und integrieren über die
Ortskoordinate des Elektrons
und integrieren über die
Ortskoordinate des Elektrons 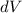
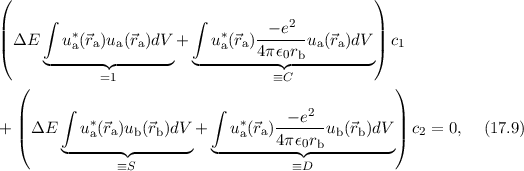
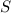 ,
, 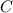 und
und 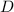 eingeführt
haben. Mit diesen Konstanten lässt sich diese Gleichung in der einfachen
Form
eingeführt
haben. Mit diesen Konstanten lässt sich diese Gleichung in der einfachen
Form

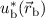 und integrieren wiederum
über die Ortskoordinate des Elektrons
und integrieren wiederum
über die Ortskoordinate des Elektrons 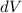 . Es ergibt sich
. Es ergibt sich
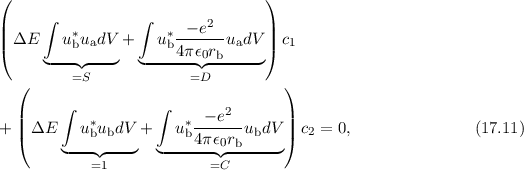

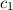 und
und 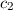 gefunden. Dieses
Gleichungssystem lässt sich in Matrixschreibweise darstellen
gefunden. Dieses
Gleichungssystem lässt sich in Matrixschreibweise darstellen
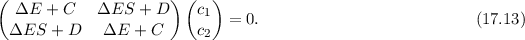


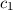 und
und 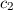 die Lösungen
die Lösungen

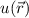 ein antisymmetrische
ein antisymmetrische 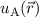 und eine symmetrische
und eine symmetrische
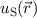 Lösung
Lösung
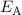 und
und 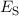 lauten
lauten

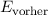 bei weit auseinander liegenden Kernen entspricht der
Grundzustandsenergie
bei weit auseinander liegenden Kernen entspricht der
Grundzustandsenergie 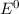 des Wasserstoffatoms. Die Gesamtenergie
des Wasserstoffatoms. Die Gesamtenergie 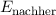 bei
nahe beieinander liegenden Kernen ergibt sich aus der Summe der Energie des
Elektrons
bei
nahe beieinander liegenden Kernen ergibt sich aus der Summe der Energie des
Elektrons 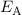 oder
oder 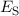 und der Coulombschen Abstossungsenergie
und der Coulombschen Abstossungsenergie 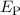 zwischen
den Protonen
zwischen
den Protonen

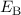 des
Wasserstoffmolekülions
des
Wasserstoffmolekülions
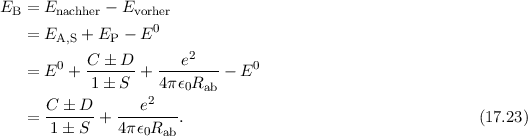
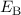 in Abhängigkeit des Abstands
in Abhängigkeit des Abstands 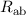 zwischen den Kernen (siehe Abb.
zwischen den Kernen (siehe Abb. 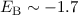 eV
bei einem Abstand
eV
bei einem Abstand 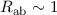 Å zwischen den Kernen (siehe Abb.
Å zwischen den Kernen (siehe Abb. 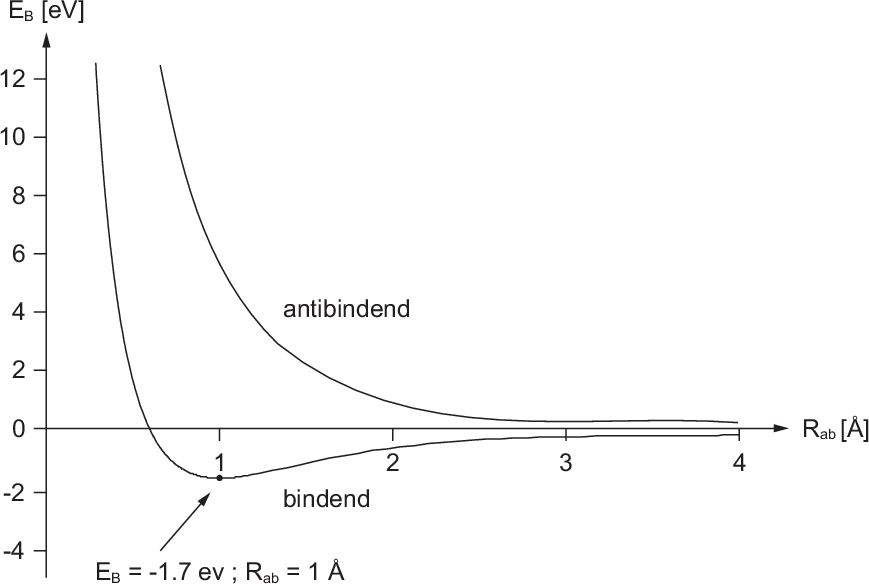
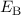 des Wasserstoffmolekülions für den
antisymmetrischen (antibindenden) und den symmetrischen (bindenden)
Zustand in Abhängigkeit des Abstands
des Wasserstoffmolekülions für den
antisymmetrischen (antibindenden) und den symmetrischen (bindenden)
Zustand in Abhängigkeit des Abstands 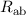 zwischen den Kernen.
zwischen den Kernen.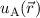 und
und 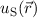 . Im symmetrischen Zustand
(siehe Abb.
. Im symmetrischen Zustand
(siehe Abb. 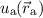 und
und 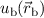 die Aufenthaltswahrscheinlichkeit für das Elektron zwischen
den beiden Kernen erhöht. Folglich hält sich das Elektron häufig zwischen
den Kernen auf, wo es die Anziehungskraft beider Kerne spürt. Dadurch
wird die potentielle Energie des Gesamtsystems gesenkt, was zur Bindung
führt. Im antisymmetrischen Zustand (siehe Abb.
die Aufenthaltswahrscheinlichkeit für das Elektron zwischen
den beiden Kernen erhöht. Folglich hält sich das Elektron häufig zwischen
den Kernen auf, wo es die Anziehungskraft beider Kerne spürt. Dadurch
wird die potentielle Energie des Gesamtsystems gesenkt, was zur Bindung
führt. Im antisymmetrischen Zustand (siehe Abb. 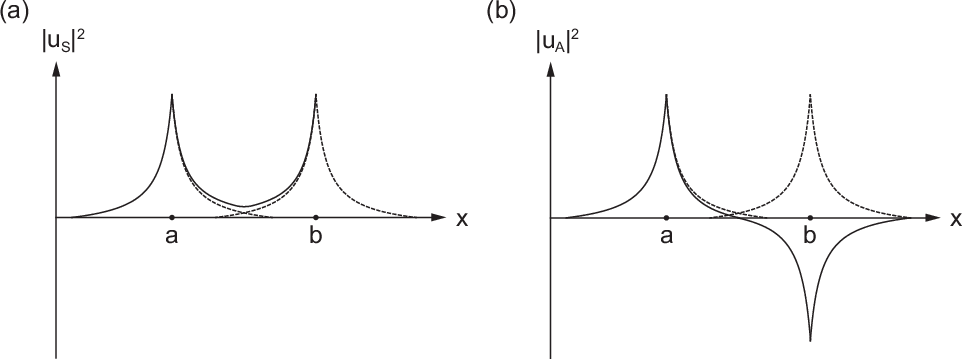
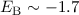 eV und den Abstand
eV und den Abstand 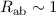 Å zwischen
den Kernen aus unserem Modell mit den experimentell bestimmten Werten
Å zwischen
den Kernen aus unserem Modell mit den experimentell bestimmten Werten
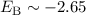 eV und
eV und 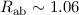 Å . Es ist zu erkennen, dass die Abweichung
der Werte relativ gross ist. Trotzdem haben wir mit unserem Modell eine
gute Vorstellung erhalten wie es zur Bindung beim Wasserstoffmolekülion
kommt.
Å . Es ist zu erkennen, dass die Abweichung
der Werte relativ gross ist. Trotzdem haben wir mit unserem Modell eine
gute Vorstellung erhalten wie es zur Bindung beim Wasserstoffmolekülion
kommt.
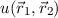 dieses Zweielektronensystems erfüllt die
Schrödinger-Gleichung
dieses Zweielektronensystems erfüllt die
Schrödinger-Gleichung

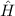 gegeben ist durch
gegeben ist durch
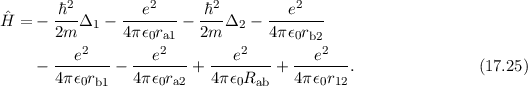
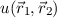 und
die Energie
und
die Energie 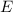 zu bestimmen. Dazu verwenden wir das
zu bestimmen. Dazu verwenden wir das 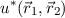 und Integration
über die Ortskoordinaten
und Integration
über die Ortskoordinaten 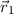 und
und 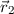 ergibt für die Energiewerte
ergibt für die Energiewerte 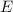 den
Ausdruck
den
Ausdruck
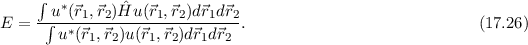
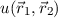 eine andere Funktion eingesetzt wird, man eine
angenäherte Lösung für die Energiewerte
eine andere Funktion eingesetzt wird, man eine
angenäherte Lösung für die Energiewerte 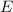 erhält oder genauer gesagt eine obere
Grenze.
erhält oder genauer gesagt eine obere
Grenze.
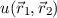 das Pauli-Prinzip
berücksichtigen, d.h. die Gesamtwellenfunktion inklusive Spins der Elektronen des
Wasserstoffmoleküls muss antisymmetrisch sein. Die erste Möglichkeit diese
Bedingung zu erfüllen, ergibt sich mit einer symmetrischen Ortswellenfunktion und
einer antisymmetrischen Spinwellenfunktion
das Pauli-Prinzip
berücksichtigen, d.h. die Gesamtwellenfunktion inklusive Spins der Elektronen des
Wasserstoffmoleküls muss antisymmetrisch sein. Die erste Möglichkeit diese
Bedingung zu erfüllen, ergibt sich mit einer symmetrischen Ortswellenfunktion und
einer antisymmetrischen Spinwellenfunktion
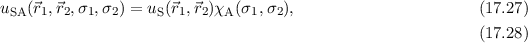
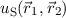 nach (
nach (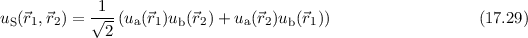
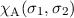 durch
durch
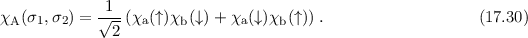
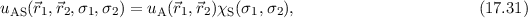
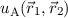 nach (
nach (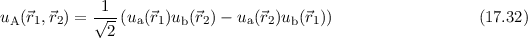
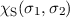 durch
durch
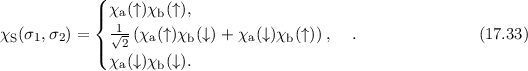
 und
und 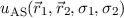 als Ansatz für die Wellenfunktion
als Ansatz für die Wellenfunktion
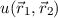 zu wählen, diese in (
zu wählen, diese in (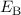 für die beiden Fälle (siehe Abb.
für die beiden Fälle (siehe Abb. 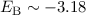 eV bei einem Abstand
eV bei einem Abstand 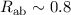 Å zwischen den Kernen.
Wiederum sind die Abweichungen zu den experimentell bestimmten Werten
Å zwischen den Kernen.
Wiederum sind die Abweichungen zu den experimentell bestimmten Werten
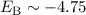 eV und
eV und 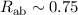 Å relativ gross. Das bedeutet, dass die
Wellenfunktion nach dem Heitler-London-Modell noch relativ ungenau sind und
zur Verbesserung des Modells noch weitere Effekte zu berücksichtigen sind.
Å relativ gross. Das bedeutet, dass die
Wellenfunktion nach dem Heitler-London-Modell noch relativ ungenau sind und
zur Verbesserung des Modells noch weitere Effekte zu berücksichtigen sind.
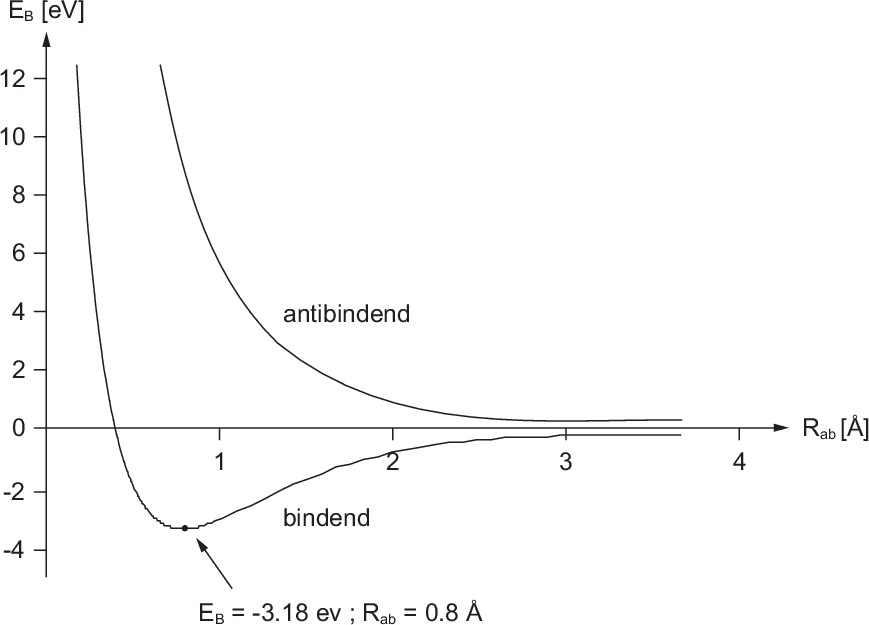
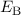 des Wasserstoffmoleküls für den
antisymmetrischen (antibindenden) und den symmetrischen (bindenden)
Zustand in Abhängigkeit des Abstands
des Wasserstoffmoleküls für den
antisymmetrischen (antibindenden) und den symmetrischen (bindenden)
Zustand in Abhängigkeit des Abstands 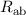 zwischen den Kernen.
zwischen den Kernen. oder das
Wassermolekül H
oder das
Wassermolekül H O gebildet werden und andere Moleküle wie das Heliummolekül
He
O gebildet werden und andere Moleküle wie das Heliummolekül
He nicht, liegt im Wesentlichen beim Pauli-Prinzip. Zum Beispiel hat
das Heliumatom im Grundzustand zwei Elektronen im
nicht, liegt im Wesentlichen beim Pauli-Prinzip. Zum Beispiel hat
das Heliumatom im Grundzustand zwei Elektronen im 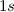 -Zustand mit
unterschiedlichem Spin. Wenn es nun mit einem anderen Heliumatom zusammen
kommt, wird jedes Heliumatom einen Teil der Zeit zwei Elektronen mit dem selben
Spin haben. Nach dem Pauli-Prinzip ist dies jedoch verboten und deshalb existiert
das Heliummolekül He
-Zustand mit
unterschiedlichem Spin. Wenn es nun mit einem anderen Heliumatom zusammen
kommt, wird jedes Heliumatom einen Teil der Zeit zwei Elektronen mit dem selben
Spin haben. Nach dem Pauli-Prinzip ist dies jedoch verboten und deshalb existiert
das Heliummolekül He nicht.
nicht.
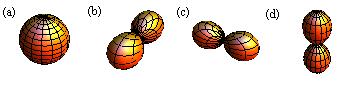
 -Zustände, (b) die
-Zustände, (b) die 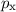 -Zustände, (c) die
-Zustände, (c) die
 -Zustände und (d) die
-Zustände und (d) die 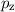 -Zustände. Gezeichnet werden jeweils Oberflächen
innerhalb derer die Aufenthaltswahrscheinlichkeit für das Elektron 90 % beträgt,
d.h.
-Zustände. Gezeichnet werden jeweils Oberflächen
innerhalb derer die Aufenthaltswahrscheinlichkeit für das Elektron 90 % beträgt,
d.h. 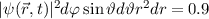 .
. -Zustände (
-Zustände (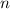 = 1, 2, 3, ...,
= 1, 2, 3, ..., 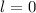 ,
, 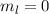 ):
):

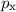 -Zustände (
-Zustände (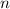 = 2, 3, 4, ...,
= 2, 3, 4, ..., 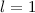 ,
, 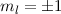 ):
):
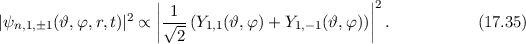
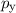 -Zustände (
-Zustände (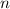 = 2, 3, 4, ...,
= 2, 3, 4, ..., 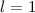 ,
, 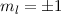 ):
):
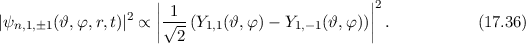
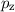 -Zustände (
-Zustände (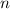 = 2, 3, 4, ...,
= 2, 3, 4, ..., 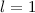 ,
, 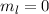 ):
):

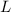 (Gesamtdrehimpuls entlang der Bindungsachse, d.h. z-Achse) mit einem griechischen
Buchstaben versehen:
(Gesamtdrehimpuls entlang der Bindungsachse, d.h. z-Achse) mit einem griechischen
Buchstaben versehen:
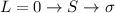
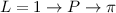
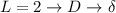
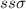 -Bindung vor. Allgemein bilden
-Bindung vor. Allgemein bilden
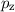 Zustände
Zustände 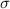 -Bindungen,
-Bindungen, 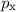 - und
- und 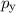 -Zustände
-Zustände 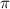 -Bindungen. Es
können auch Bindungen aus Zuständen, die zu unterschiedlichen Drehimpulsen
gehören, gebildet werden. Ein Beispiel ist das Wassermolekül. Die zwei einfach
besetzten
-Bindungen. Es
können auch Bindungen aus Zuständen, die zu unterschiedlichen Drehimpulsen
gehören, gebildet werden. Ein Beispiel ist das Wassermolekül. Die zwei einfach
besetzten 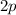 -Zustände des Sauerstoffatoms kommen mit den
-Zustände des Sauerstoffatoms kommen mit den 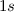 -Zuständen
der Wasserstoffatome zusammen und bilden jeweils eine
-Zuständen
der Wasserstoffatome zusammen und bilden jeweils eine 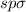 -Bindung.
Dabei bewirkt die gegenseitige Abstossung zwischen den Wasserstoffatomen
eine Vergrösserung des Winkels zwischen den Bindungsachsen von 90
-Bindung.
Dabei bewirkt die gegenseitige Abstossung zwischen den Wasserstoffatomen
eine Vergrösserung des Winkels zwischen den Bindungsachsen von 90 zu
104.5
zu
104.5 .
.
 zeigt. Man würde nämlich erwarten, dass das Kohlenstoffatom mit einer
Elektronenkonfiguration
zeigt. Man würde nämlich erwarten, dass das Kohlenstoffatom mit einer
Elektronenkonfiguration 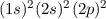 mit zwei Wasserstoffatomen ein CH
mit zwei Wasserstoffatomen ein CH Molekül mit zwei
Molekül mit zwei 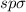 -Bindungen unter einem Bindungswinkel von etwas mehr als
90
-Bindungen unter einem Bindungswinkel von etwas mehr als
90 bildet. In der Natur kommt aber auch das Methan-Molekül CH
bildet. In der Natur kommt aber auch das Methan-Molekül CH vor, das perfekt symmetrisch ist mit vier exakt gleichen C-H-Bindungen. Es
stellt sich jetzt natürlich die Frage, wie ist eine solche Bindung möglich. Die
Antwort ist, dass es beim Kohlenstoffatom zur Bildung von Superpositionen aus
dem
vor, das perfekt symmetrisch ist mit vier exakt gleichen C-H-Bindungen. Es
stellt sich jetzt natürlich die Frage, wie ist eine solche Bindung möglich. Die
Antwort ist, dass es beim Kohlenstoffatom zur Bildung von Superpositionen aus
dem 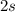 -Zustand und den drei
-Zustand und den drei 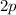 -Zuständen zu vier neuen Zuständen
(
-Zuständen zu vier neuen Zuständen
(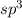 -Zustände) kommt. Dieses Phänomen wird
-Zustände) kommt. Dieses Phänomen wird 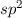 -Zustände (ein Elektron bleibt im
-Zustände (ein Elektron bleibt im 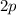 -Zustand,
die übrigen drei besetzen hybridisierte Zustände) und
-Zustand,
die übrigen drei besetzen hybridisierte Zustände) und 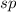 -Zustände (zwei
Elektronen bleiben im
-Zustände (zwei
Elektronen bleiben im 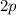 -Zustand, die übrigen zwei besetzen hybridisierte
Zustände).
-Zustand, die übrigen zwei besetzen hybridisierte
Zustände).
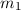 und
und 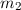 und einen Abstand von
und einen Abstand von 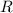 ,
sowie jeweils einen Abstand von
,
sowie jeweils einen Abstand von 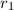 bzw.
bzw. 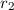 zum Schwerpunkt.
zum Schwerpunkt.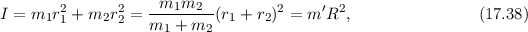

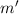 um eine Achse mit
Abstand
um eine Achse mit
Abstand 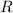 . Der Betrag des Drehimpulses
. Der Betrag des Drehimpulses 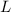 des Moleküls ist gegeben
durch
des Moleküls ist gegeben
durch

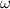 die Winkelgeschwindigkeit ist. Wie immer ist der Drehimpuls quantisiert,
d.h. es gilt
die Winkelgeschwindigkeit ist. Wie immer ist der Drehimpuls quantisiert,
d.h. es gilt

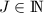 eingeführt haben. Damit ergibt sich für
die Rotationsenergie
eingeführt haben. Damit ergibt sich für
die Rotationsenergie
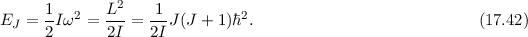
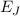 . Für die Übergangsfrequenzen
. Für die Übergangsfrequenzen  gilt
gilt


 oder Kohlenstoffdioxid
CO
oder Kohlenstoffdioxid
CO .
.
 proportional zur Rotationsquantenzahl
proportional zur Rotationsquantenzahl
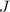 . Aus diesem Grund sind im Spektrum eines Moleküls äquidistante Spektrallinien
zu beobachten.
. Aus diesem Grund sind im Spektrum eines Moleküls äquidistante Spektrallinien
zu beobachten.
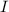 eines Moleküls bestimmt werden. Sind zudem die Massen
eines Moleküls bestimmt werden. Sind zudem die Massen 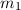 und
und 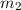 der
beteiligten Atome bekannt, ergibt sich mit (
der
beteiligten Atome bekannt, ergibt sich mit (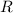 des
Moleküls.
des
Moleküls.

 eingeführt haben und nur die Übergänge,
die die Auswahlregel
eingeführt haben und nur die Übergänge,
die die Auswahlregel 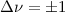 erfüllen, zugelassen sind. In der Realität ist der
Abstand der Energieniveaus der Molekülschwingung nicht äquidistant, sondern
nimmt für hohe Energien ab. Der Grund dafür liegt darin, dass für hohe Energien die
Beschreibung durch den harmonischen Oszillator nicht mehr gerechtfertigt
ist.
erfüllen, zugelassen sind. In der Realität ist der
Abstand der Energieniveaus der Molekülschwingung nicht äquidistant, sondern
nimmt für hohe Energien ab. Der Grund dafür liegt darin, dass für hohe Energien die
Beschreibung durch den harmonischen Oszillator nicht mehr gerechtfertigt
ist.
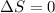 für die Spinquantenzahl sehr unwahrscheinlich in den
Grundzustand zurück und das Molekül verweilt in einem sogenannte metastabilen
Zustand
für die Spinquantenzahl sehr unwahrscheinlich in den
Grundzustand zurück und das Molekül verweilt in einem sogenannte metastabilen
Zustand